Berechnen Sie die Beträge folgender Vektoren:

Question

Aufgabe:

Problem/Ansatz: ich brauche Hilfe bei Aufgabe 3b und 4f

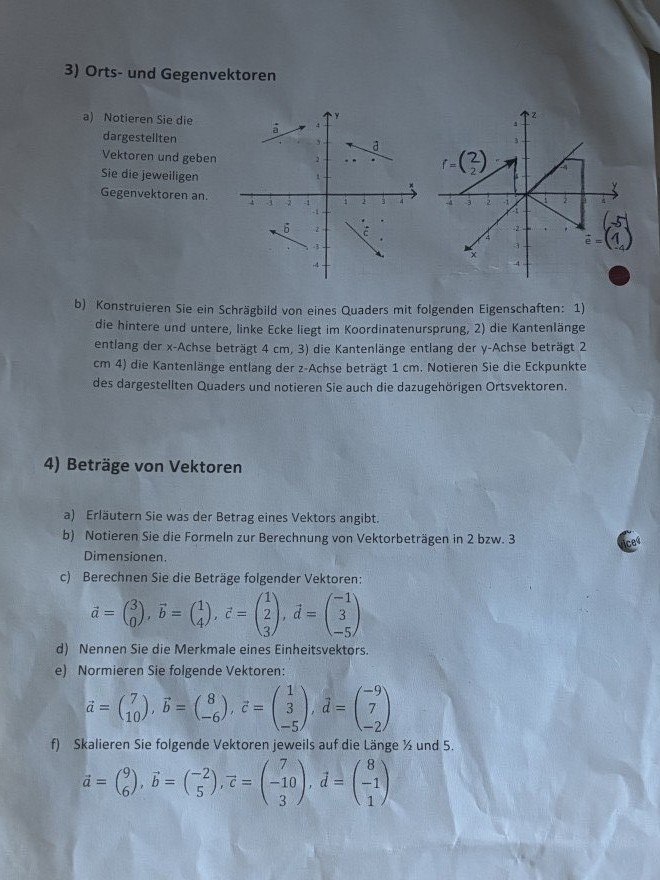
Text erkannt:

3) Orts- und Gegenvektoren
a) Notieren Sie die dargestellten Vektoren und geben Sie die jeweiligen Gegenvektoren an.
b) Konstruieren Sie ein Schrägbild von eines Quaders mit folgenden Eigenschaften: 1) die hintere und untere, linke Ecke liegt im Koordinatenursprung, 2) die Kantenlänge entlang der \( x \)-Achse beträgt \( 4 \mathrm{~cm}, 3 \) ) die Kantenlänge entlang der \( y \)-Achse beträgt 2 \( \mathrm{cm} 4) \) die Kantenlänge entlang der \( z \)-Achse beträgt 1 cm . Notieren Sie die Eckpunkte des dargestellten Quaders und notieren Sie auch die dazugehörigen Ortsvektoren.
4) Beträge von Vektoren
a) Erläutern Sie was der Betrag eines Vektors angibt.
b) Notieren Sie die Formeln zur Berechnung von Vektorbeträgen in 2 bzw. 3

vices

Dimensionen.
c) Berechnen Sie die Beträge folgender Vektoren:
\( \vec{a}=\binom{3}{0}, \vec{b}=\binom{1}{4}, \vec{c}=\left(\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right), \vec{d}=\left(\begin{array}{c} -1 \\ 3 \\ -5 \end{array}\right) \)
d) Nennen Sie die Merkmale eines Einheitsvektors.
e) Normieren Sie folgende Vektoren:
\( \vec{a}=\binom{7}{10}, \vec{b}=\binom{8}{-6}, \vec{c}=\left(\begin{array}{c} 1 \\ 3 \\ -5 \end{array}\right), \vec{d}=\left(\begin{array}{c} -9 \\ 7 \\ -2 \end{array}\right) \)
f) Skalieren Sie folgende Vektoren jeweils auf die Länge \( 1 / 2 \) und 5 .
\( \vec{a}=\binom{9}{6}, \vec{b}=\binom{-2}{5}, \vec{c}=\left(\begin{array}{c} 7 \\ -10 \\ 3 \end{array}\right), \vec{d}=\left(\begin{array}{c} 8 \\ -1 \\ 1 \end{array}\right) \)

Comments

Wenn Du die anderen kannst, was ist hier dann das Problem?

---

Eine Antwort auf diese problemdiagnostisch ganz herausragende Frage würde auch mich interessieren. Denn ich bin verwirrt, auch weil das, was in Deinem Titel steht, weder bei 3b noch bei 4f verlangt wird.

Answer 1

3. b)

4. f)

Achtung: Ich normiere hier nur auf die Länge 1/2 = 0.5. Für die Länge 5 einfach statt 0.5 die 5 nehmen.

$$\frac{0.5}{\sqrt{9^2 + 6^2}} \cdot \begin{pmatrix} 9\\6 \end{pmatrix} = \frac{\sqrt{13}}{26} \cdot \begin{pmatrix} 3\\2 \end{pmatrix} \newline \frac{0.5}{\sqrt{2^2 + 5^2}} \cdot \begin{pmatrix} -2\\5 \end{pmatrix} = \frac{\sqrt{29}}{58} \cdot \begin{pmatrix} -2\\5 \end{pmatrix} \newline \frac{0.5}{\sqrt{7^2 + 10^2 + 3^2}} \cdot \begin{pmatrix} 7\\-10\\3 \end{pmatrix} = \frac{\sqrt{158}}{316} \cdot \begin{pmatrix} 7\\-10\\3 \end{pmatrix} \newline \frac{0.5}{\sqrt{8^2 + 1^2 + 1^2}} \cdot \begin{pmatrix} 8\\-1\\1 \end{pmatrix} = \frac{\sqrt{66}}{132} \cdot \begin{pmatrix} 8\\-1\\1 \end{pmatrix}$$