Eigenmann-Aufgabe: Habt Ihr auch für den Winkel mü 135° raus? Im Lösungsbuch steht, dass 100° richtig sei.

Question

Aufgabe:

Problem/Ansatz:

Hey Leute und zwar wollte ich euch fragen, ob ihr ebenfalls für den Winkel mü 135 grad raus bekommt. Im Lösungsbuch steht jedoch, dass der Winkel 100 grad sei. Deswegen weiß ich jetzt nicht wo mein Fehler ist. Ich hab halt Hilfslinien eingezeichnet um den Satz des Thales zu verwenden. Ihr habt einmal die Aufgabe

Comments

Ich halte 100 Grad für richtig.

Thales wird nicht benötigt.

---

Warum sollten die roten 45° und die lilanen 45° gleich sein? Man sieht doch eindeutig, dass das Dreieck nicht gleichschenklig ist.

---

Mein Geodreieck legt auch 100° nahe.  :-)

---

Alles klar, vielen Dank euch:)

Kann man nicht eure Kommentare mehr liken? Als Dankeschön. Finde kein Daumenhoch

---

Ich schreibe diesen Monat nur Kommentare, keine Antworten. Aber es wird in nützlicher Frist wohl jemand dasselbe nochmals als Antwort einstellen. Die kannst Du dann daumenhochen, bei Bedarf.

Das mit dem Geodreieck würde ich nicht als Lösungsweg verwenden. Denn es soll hier begründet werden, nicht gemessen. Die eigenmannsche Zeichnung ist auch nicht maßstabgetreu, was man sieht wenn man 10-Grad-Winkel und 40-Grad-Winkel miteinander vergleicht. Das sind seine Zeichnungen meistens nicht, und zwar absichtlich.

---

Ich schreibe diesen Monat nur Kommentare, keine Antworten.

Warum?

---

Warum?

Das war ja eine schlagfertige Reaktion auf meine Aussage, dass ich diesen Monat keine Antworten gebe, höchstens Kommentare.

Answer 1

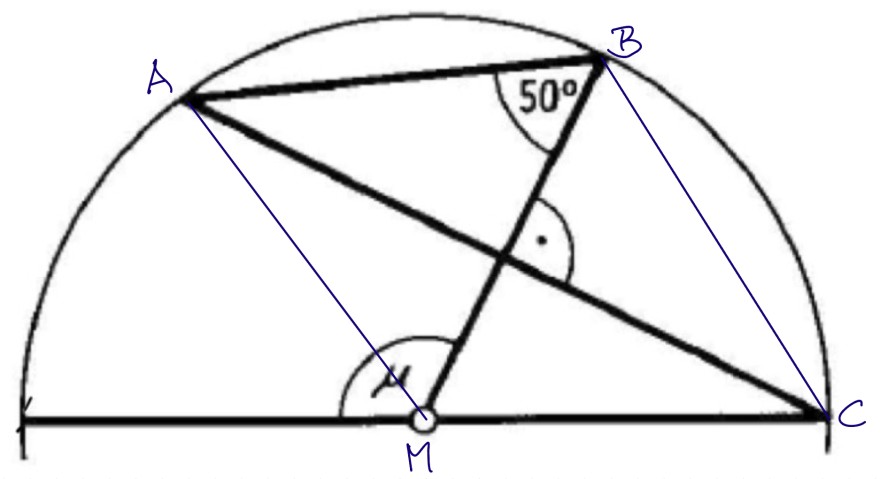
Beachte, dass das Dreieck AMC gleichschenklig ist und durch die Höhe in zwei kongruente Dreiecke zerlegt wird.

Dadurch wird das Viereck AMCB zu einem Drachen, bei dem die Diagonalen senkrecht aufeinander stehen und eine Diagonale durch die andere halbiert wird.

Aus Symmetriegründen hat das gleichschenklige Dreieck ACB an der Spitze einen Winkel von 100 Grad und an der Basis zwei Winkel von je 40 Grad.

Soweit warst du ja bereits selber.

Nun ist das Dreieck CBM auch gleichschenklig. Damit sind die Basiswinkel bei B und C mit 50 Grad gleich groß und der Winkel an der Spitze M beträgt 80 Grad.

Damit hat der gesuchte Winkel, der ja ein Nebenwinkel des Winkels von 80 Grad ist, einen Winkel von 100 Grad.