a)
Kennt ihr das Kreuzprodukt bzw. die Bedeutung des Kreuzproduktes. Darauf beruht die Abstandsformel eines Punktes von einer Geraden.
Benutze ich die, erhalte ich als Ansatz
|([x, 0, 0] - [0, 11, 3]) ⨯ [0, 1, 1]| / |[0, 1, 1]| = 9
Damit erhalte ich x = ±7
Die Punkte sind also bei (±7 | 0 | 0)
b)
Die Gerade verläuft in der yz-Ebene. Die x-Achse verläuft senkrecht zur yz-Ebene. Damit hat auf der x-Achse der Punkt der ebenfalls in der yz-Ebene liegt, den kleinsten Abstand. Das ist der Koordinatenursprung.
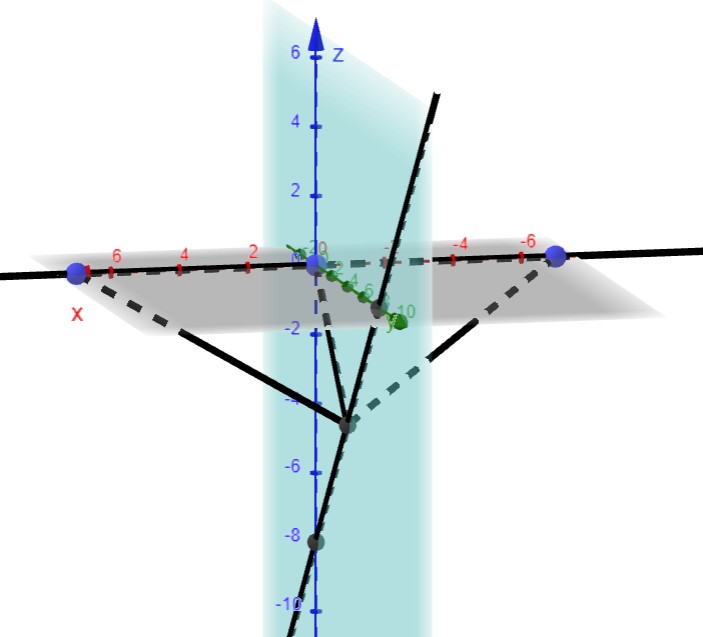
Vielleicht hilft es dir, sich das bei Geogebra zu visualisieren: