Aufgabe #145/1 von Eigenmann

Question

Aufgabe:

Eigenmann-Aufgabe 145/1

Ohne Taschenrechner; die Figuren sind nicht maßgetreu.

Paul Eigenmann, Aufgabe 1.4.145, ISBN 3-12-722310-2, 1981, S. 22.

Comments

Eigenmann hat auch Lösungen mitgeliefert. Zu dieser Aufgabe schrieb er:

[spoiler]

\(\displaystyle 72^\circ \)

[/spoiler]

(eingangs zitiertes Werk, S. 57)

Answer 1

Kleiner Tipp: Zeichne dir mal alle gleichschenkligen Dreiecke ein.

α = 72°

Comments

Und gülden glänzt der Schnitt...

---

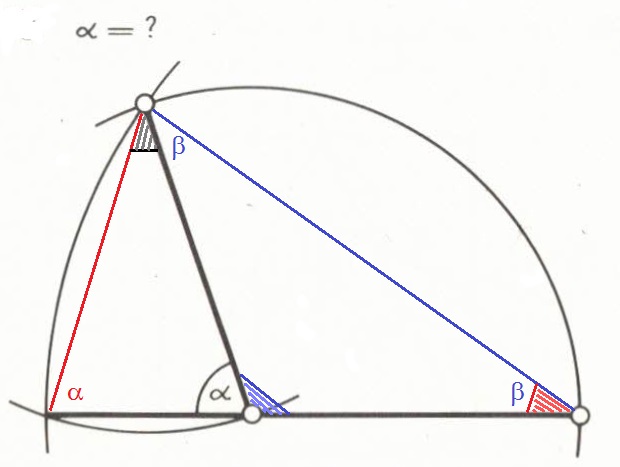
Mit 2 zusätzlichen Geraden entstehen 3 gleichschenklige Dreiecke (ausgehend von je einem Zirkel-Einstechpunkt). Im linken Dreieck ist der Winkel  links unten α wie rechts daneben,

Beim oberen Einstechpunkt ist die Summe der beiden Winkel auch α ( der zweite Winkel an der Basis des von rechts ausgehenden gleichschenkligen Dreiecks).
(180° - 2α) + β = α 

Die Winkel  α und  β  sind auch im von Mitte unten ausgehenden gleichschenkligen Dreieck enthalten.
(180° -  α)  + 2β  = 180°   >>   β = α/2 .

Mit  β = α/2  in obiger  Beziehung folgt
(180° - 2α) + α/2 = α   >>   α = 2/5 • 180° = 72 ° .

---

Was ich schon seit Monaten mit Verwunderung feststelle:

Selbst die kompetentesten Leute gehen bei Aufgaben dieser Art immer wieder den

"180°-α" -Umweg.

Es gibt den Außenwinkelsatz!!!

Damit gilt SOFORT β+β=α bzw. β=α/2.

Wenn -wie du schon schriebst- alle abgebildeten Dreiecke gleichschenklig sind, tritt der Winkel α auch oben im Gesamtdreieck auf, dessen Innenwinkelsumme dann α+α+α/2=180° ist. So kommt man viel schneller auf α=72°

---

Abakus

"180°-α" -Umweg.

Danke für den Hinweis auf den Außenwinkelsatz. Ich halte mein Vorgehen nicht als gravierendes Manko. Der Satz folgt ja doch sofort aus dem "Umweg", ist für das Dreieck lediglich die Kurzformulierung. Ich komme damit und sogar sehr schnell weiter, ohne dass ich einen verzichtbaren Satz gepaukt haben muss (der schulmässig anzuwenden, aber oft nicht begriffen ist). Zusammengefasst: Bei der vorliegenden Aufgabe wäre mit zwei Zeilen Rechnung anstatt drei auszukommen gewesen.

Im Allgemeinen schätze ich Deine Einfälle und deren Verwertung sehr. Bei der 4/9-Idee hätte ich den Button "Beste" gern gedrückt, wenn man mir ihn nur angeboten hätte.

---

Ich halte mein Vorgehen nicht als gravierendes Manko.

Ich auch nicht. Der Außenwinkelsatz gehört hier in Hamburg auch nicht zum Bildungsplan.

Wie man sieht, dauert es zwar länger, aber man braucht den Satz eben nicht unbedingt.

Tipp: Da der Außenwinkelsatz hier bei den Eigenmann-Aufgaben allerdings schon mehrmals angesprochen wurde, würde ich den evtl. mal in die eigene Formelsammlung aufnehmen, wenn er da nicht bereits vorhanden ist.

---

ohne dass ich einen verzichtbaren Satz gepaukt haben muss

Das ist jetzt auch kein Satz, den man pauken muss, sondern der sehr leicht nachvollziehbar ist. Wenn er einem mal begegnet, was ja nun hier bei den Eigenmann-Aufgaben der Fall ist, kann man ihn sicherlich in sein Repertoire aufnehmen.