Aufgabe:
Es sei \( \Omega=] 0,1\left[\right. \) das offene Einheitsintervall. Für \( n \in \mathbb{N}_{0} \) sei \( A_{n}:=\left[\frac{1}{2^{n+1}}, \frac{1}{2^{n}}[\right. \). Des weiteren definieren wir \( \mathcal{E}:=\left\{A_{n} \mid n \in \mathrm{N}_{0}\right\} \)
(a) Zeigen Sie, dass \( \sigma(\mathcal{E})=\left\{\bigcup_{n \in I} A_{n} \mid I \subseteq \mathbb{N}_{0}\right\} \).
(b) Welche der folgenden Mengen sind Elemente von \( \sigma(\mathcal{E}) \) ? (Keine schriftliche Begründung nötig.) \( A:=\{1 / 2\}, \quad B:=[1 / 4,1[, \quad C:=[1 / 3,2 / 3[, \quad D:= ] 0,1 / 2[ \).
Nachtrag Definition:
1.2.10 Satz
Desweiteren ist \( \sigma(\mathcal{E}) \) die kleinste \( \sigma \) -Algebra auf \( \Omega \), die \( \varepsilon \) enthält.
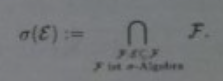
1.2.11 Definition (Borel-\( \sigma \)-Algebra)
Sei \( (\Omega, \mathcal{O}) \) ein topologischer Raum. Das bedeutet, dass \( O \subseteq \mathcal{P}(\Omega) \) abgeschlossen bezüglich beliebiger Vereinigungen und endlichen Durchschnitten ist. Die Elemente von \( O \) heißen offen. Dann definieren wir die Borel-\( \sigma \)-Algebra auf \( (\Omega, \mathcal{O}) \) durch
\( B(\Omega):=\mathcal{B}((\Omega, O)):=\sigma(O) \)
1.2.12 Satz
Sei \( O \) die von \( (a, b) \subseteq 0,1] \) erzeugte Topologie auf \( [0,1] \). Dann existiert genau ein \( W-M \) \( P \) auf \( (0,1), \sigma(\mathcal{O}))=(\Omega, \mathcal{F}) \) mit \( (1.2) \). Dieses erfüllt auch \( (1.3) \). Dieses Maß nennen wir Lebesgue-Maß auf [0, 1], uniforme Verteilung auf [0, 1] oder Gleichverteilung auf [0, 1].
Beweis:
Um diesen Satz zu beweisen, müssen wir die Existenz und die Eindeutigkeit nachweisen.
(1) Die Existenz wird in Analysis 3 bewiesen.
(2) Die Bindeutigkeit folgt aus dem Maffeindeutigkeitssatz (1.2.13).
Damit haben wir die Behauptungen des Satzes bewiesen.