f(x)=x3+kx2+2
1. Ableitung ist: f'(x)=3*x2+2*k*x
Null setzen zum Finden der Extrempunkte: 3*x2+2*k*x = 0
// x ausklammern
x*(3*x+2*k) = 0
Die erste Nullstelle ist bei x1 = 0
Die zweite Nullstelle (den Term in Klammern null setzen):
3*x+2*k = 0 | - 2*k
3*x = -2*k | :3
x = -2/3*k
Die zweite Nullstelle ist bei x2 = -2/3*k
Dich interessiert die erste Nullstelle mit x1 = 0.
Dieses setzt du in die Funktionsgleichung ein und erhältst:
f(x)=x3+kx2+2
f(0)=03+k*02+2 = 2
→ P(0 | 2)
Hier sind einige Funktionsgraphen mit Beispielwerten k=1, k=2, k=-3. Alle Funktionen haben einen Extrempunkt bei P(0|2):
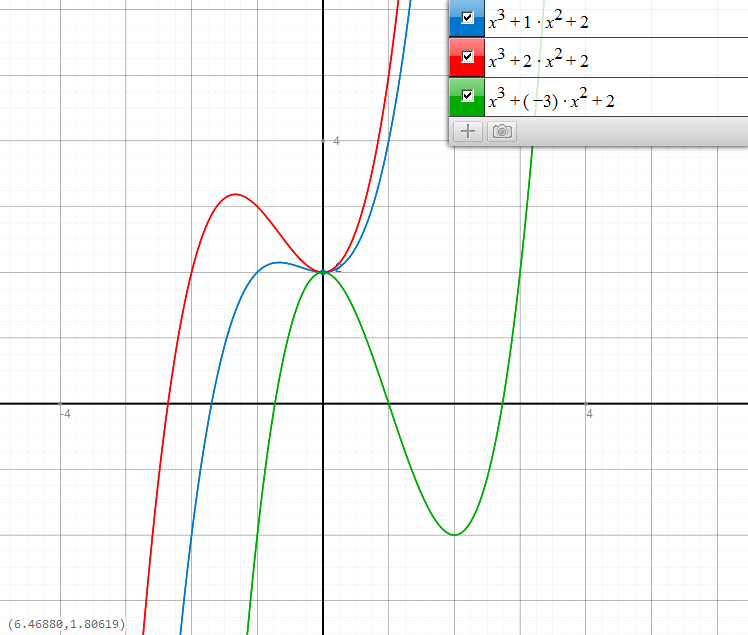
Da hier ein Parameter k gegeben ist, der die Funktion verändert, fällt das ganze Thema unter das Stichwort: Funktionsscharen bzw. Kurvenscharen.