Minimaler und maximaler Winkel im dreidimensionalen kartesischen Koordinatensystem

Question

Ein quadratisches Messegelaende liegt in der x1-x2-Ebene und hat den Mittelpunkt (3/3/0). Die Quadratseiten sind parallel zu den Koordinatenachsen und haben die Laenge 2km. Bei einer Flugschau haben die Zuschauer auf dem Messegelaende die Moeglichkeit Flugzeuge zu beobachten.

a) Unter welchem maximalen und unter welchem minimalen Winkel zur Horizontalen kann von diesem Messegelaende aus ein Flugzeug bertrachtet werden, das sich gerade im Punkt F(6/6/1) befindet

Answer 1

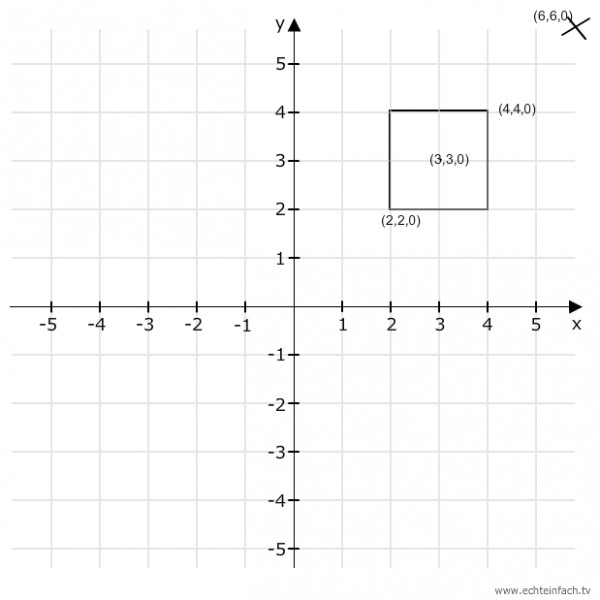
Skizze am Boden:

(4,4,0) ist am nächsten beim Flugzeug. Der Winkel ist dort am grössten.

(2,2,0) ist am weitesten weg. Der Winkel ist am kleinsten.

Winkel kannst du mit dem Skalarprodukt berechnen, wenn 3-dim Vektoren bekannt sind.

cos (Zwischenwinkel) = uv/(|u||v|)

Grösster Winkel. u = (2,2,0), v=(2,2,1) 

cos ALPHA = (4+4+0)/ (√8 *3 ) 

ALPHA = 19.47° über dem Horizont

 

Kleinster Winkel. u = (4,4,0), v=(4,4,1) 

cos BETA = (16+16+0)/ (√32 *√33 ) 

BETA = 10.02° über dem Horizont

Wenn das Skalarprodukt noch unbekannt ist, zeichnest du rechtwinklige Schnittdreiecke und benutzt Pythagoras sowie die Winkelfunktionen. Sollte auch klappen.

Answer 2

Eine kleine Skizze hilft beim Rechnen. Es ist unklar ob eine Einheit in der Aufgabe auch 1 km entspricht. Ich gehe mal davon aus.

Skizze:

Den minimalen Abstand zum Flugzeug haben wir im Punkt (4 | 4). Der Abstand in der Ebene beträgt dann 

Wurzel(2^2 + 2^2) = Wurzel(8)

Der Winkel unter dem man das Flugzeug sieht berechnet sich dann mit

Alpha = arctan(Höhendifferenz / Differenz in der Ebene) = arctan(1 / Wurzel(8)) = 19,47 Grad

 

 

Den maximalen Abstand zum Flugzeug haben wir im Punkt (2 | 2). Der Abstand in der Ebene beträgt dann 

Wurzel(4^2 + 4^2) = Wurzel(32)

Der Winkel unter dem man das Flugzeug sieht berechnet sich dann mit

Alpha = arctan(Höhendifferenz / Differenz in der Ebene) = arctan(1 / Wurzel(32)) = 10,02 Grad