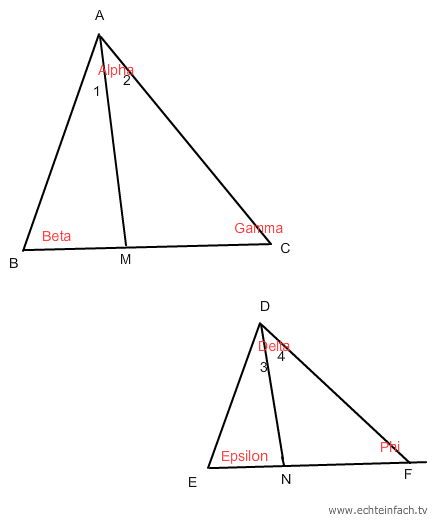
9. Für die Dreiecke auf dem Foto gilt: ΔABM ~ ΔDEN (ähnliche Dreiecke),
D.h. sie stimmen in der 3 Winkeln überein. Insbesondere gilt ∠ 1 = ∠ 3. ∠ Beta = ∠ Epsilon.
Folgende Winkel entsprechen sich: ∠ 1 ≅ ∠ 2, und ∠ 3 ≅ ∠ 4.
Wegen ∠ 1 = ∠ 3 gilt ∠ 2 = ∠ 4
Beweise, dass ΔABC ~ ΔDEF.
Zu zeigen ist: Diese beiden Dreiecke haben die gleichen Winkel.
∠ Beta = ∠ Epsilon
∠ Alpha = ∠ 1 + ∠ 2 = ∠ 3 + ∠ 4 = ∠ Delta
Da die Winkelsumme im Dreieck 180° ist, gilt
∠ Gamma = 180° -∠ Alpha - ∠ Beta = 180° - ∠ Delta - ∠ Epsilon = ∠ Phi
was zu beweisen war
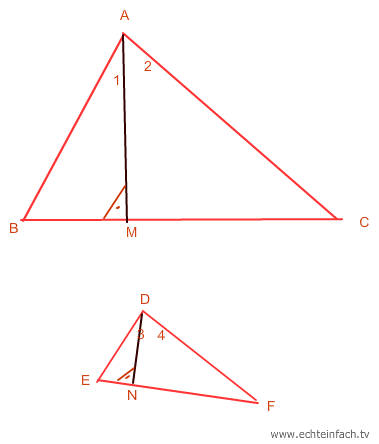
11. Gegeben zwei Dreiecke ABC und DEF so dass ΔABC ~ ΔDEF (ähnliche Dreiecke). Punkt M liegt zwischen B und C so dass
AM⊥ BC (senkrecht) und Punkt N liegt zwischen E und F so dass DN⊥EF (senkrecht). Beweise, dass
BM / EN = MC / NF
Beweis: Beta = Epsilon und beide Dreiecke einen rechten Winkel enthalten, sind alle 3 Winkel gleich. Also auch 1 und 3:
ΔABM ~ ΔDEN
ergänzend dazu sind Phi = Gamma, 90°=90° daher: 2 und 4 gleich. Deshalb ΔAMC ~ ΔDNF.
Die Verhältnisse entsprechender Strecken in 2 ähnlichen Dreiecken sind gleich.
Deshalb:
ΔABM ~ ΔDEN ------> | BM| / |EN| = |AM| / |DN|
ΔAMC ~ ΔDNF → |MC| / |NF| = |AM| / |DN|
Nun die beiden Gleichungen verknüpfen
|BM| / |EN| = |AM| / |DN| = |MC| / |NF|
Also: |BM| / |EN| = |MC| / |NF|
was zu beweisen war.
Ich hoffe jetzt mal, dass du das so weit verstehst und es zurückübersetzen kannst ins Englische.