Frage : komplexe zahlen ebene

Question

Komplexe Zahlenebene

Skizzieren Sie als als Punktmengen in der komplexen Zahlenebene die folgenden Mengen und begründen Sie kurz Ihre Lösungen:

\( \begin{array}{c} \left\{z \in \mathbb{C} \mid z=2-i+2 e^{i t}, \pi / 2 \leq t \leq \pi\right\}, \quad\left\{z \in \mathbb{C} \mid z^{7}=1\right\} \\ \{z \in \mathbb{C}||(1+i) z+1-i \mid=5\}, \quad\left\{z \in \mathbb{C} \mid \operatorname{Im}\left(z^{2}\right) \leq 2\right\} \end{array} \)

Answer 1

Hi,

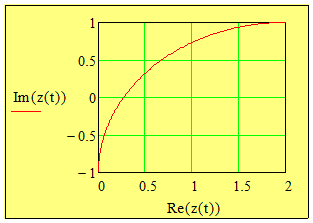
zur ersten Aufgabe. Der Term \( e^{it}  \) beschreibt einen Viertelkreis, der bei (0,i)  anfängt und bei (-1,0) aufhört, da das ganze noch mit zwei multipliziert wird, fängt der Viertelkreis jetzt bei (0,2i) an und hört bei (-2,0) auf. Jetzt wird noch auf den Realteil 2 hinzu addiert und beim Imaginärteil i abgezogen, also ist das ganze ein Viertelkreis mit Radius 2 der bei (0,-i) beginnt und bei (2,i) aufhört.

Zur zweiten Aufgabe
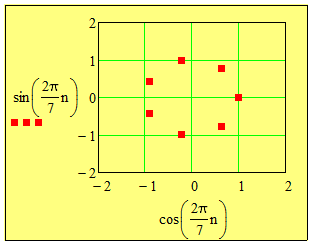
Da man jede komplexe Zahl  schreiben kann \( z=re^{i\phi} \) gilt \( z^7=r^7e^{7i\phi}=1 \) Daraus folgt erstmal das \( r=1 \) gilt. Also haben wir noch die Gleichung \( e^{7i\phi}=1 \) zu lösen für \(\phi\). Der Realteil von \( e^{7i\phi} \) wird 1, wenn \( 7\phi=2\pi n \) gilt. ALso ist \( \phi = \frac{2\pi}{7}n \). Hier für gibt es 7 verschiedene Lösungen, nämlich für n=0..6

Vielleicht schaffts Du ja den Rest alleine.