Berechnen Sie, wo im angegebenen Definitionsbereich die Funktionen (un)stetig sind. f(x) = arccos x, g(x)=(x+1)/(x-1)

Question

Berechnen Sie, wo im angegebenen Definitionsbereich folgenden Funktionen stetig sind und wo nicht:

$$ f(x) = arccos x \qquad für x ∈[-1,1] $$

$$ g ( x ) = \left\{ \begin{aligned} \frac { x + 1 } { x - 1 } , & \text { falls } x \neq 1 \\ 0 & \text { falls } x = 1 \end{aligned} \right. , \text { falls } x \neq 1 $$

Answer 1

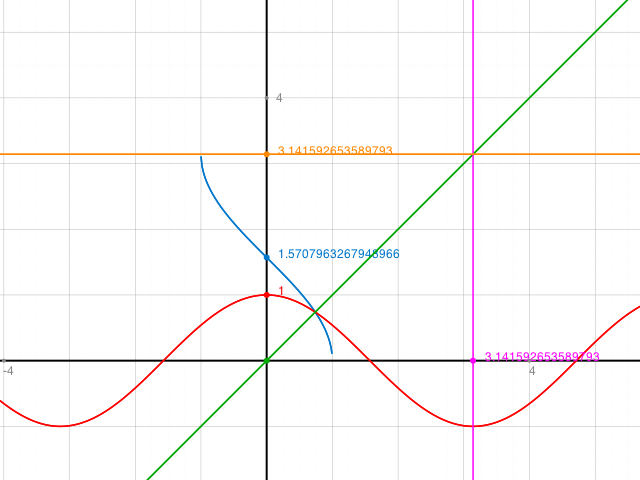
arccos x (blau) ist die Umkehrfunktion von cos x (rot eingeschränkt auf das Intervall von 0 bis pi)

Man erhält blau aus rot durch eine Spiegelung an y=x (grün)

blau ist im Intervall von [-1,1] stetig, da auch rot stetig ist.

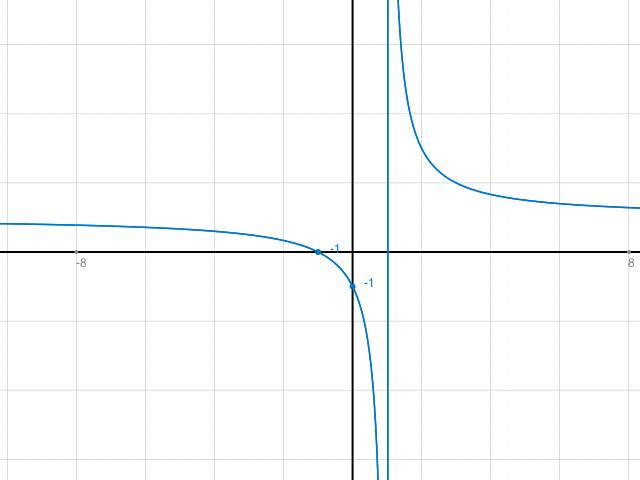
g(x) (blau) mit einem Punkt bei (1/0) ist überall stetig ausser in x = 1.

Zum Berechnen macht man am besten eine Wertetabelle, wenn man die Graphen der Funktionen nicht kennt.

Beim Ersten wie gesagt Spiegelung an y=x. Beim 2. Graph: g(x) = (x+1)/(x-1) hat einen Pol (nicht hebbare Nullstelle im Nenner) in x =1.

y = x + 1 ist stetig, ebenso x-1. Deshalb auch (x+1)/(x-1) wenn nicht gerade durch 0 dividiert wird. Also ausser in x =1.