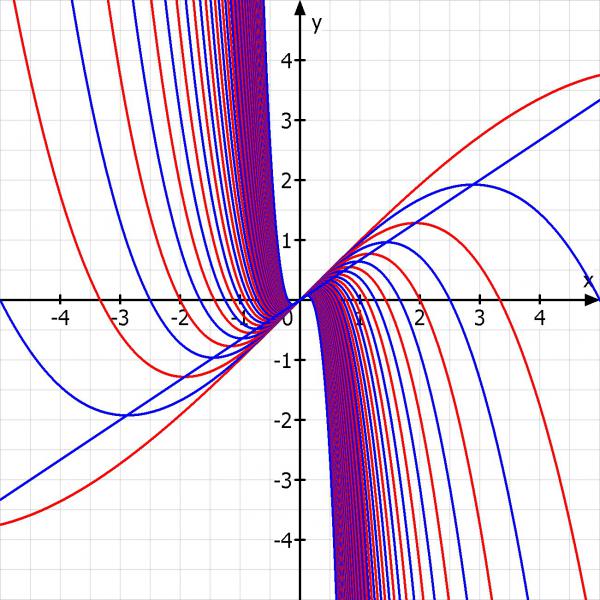
fa(x) = x - a^2 * x^3
Extremstelle bei
fa'(x) = 1 - 3 * a^2 * x^2 = 0
Damit bei x ein Extrema ist muss für a gelten:
1 - 3 * a^2 * x^2 = 0
a = ±√3/(3·x)
Das setzte ich in die Funktionsgleichung ein.
f(x) = x - a^2 * x^3 = x - (√3/(3·x))^2 * x^3 = 2/3·x
Auf dem Graphen liegen die Extrema
Skizze: