Punktsymmetrie und Achsensymmetrie

Question

Wie kann ich Punkt- und Achsensymmetrie voneinander unterscheiden?

Vielleicht am besten mit Skizze, Danke

Answer 1

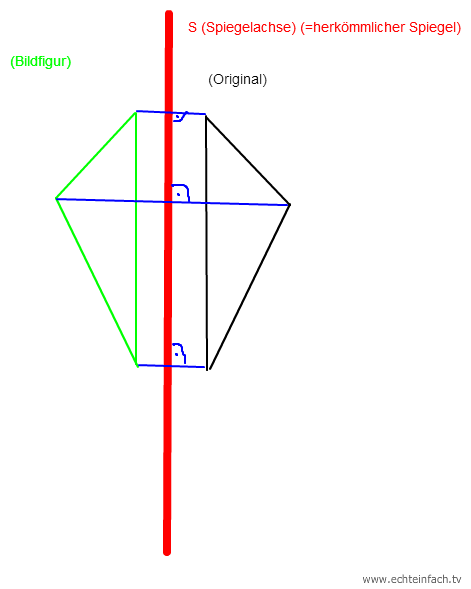
Die Achsenspiegelung ist wie wenn man die Figur vor einen Spiegel halten würde. Die Figur dreht sich aber nicht. Wenn du die entsprechenden Punkte verbindest, stehen die Geraden senkrecht zur Spiegelachse.

Dagegen dreht die Punktspiegelung die Figur um 180°. Dies ist eine Zentrische Streckung mit dem Faktor -1. Auch siehst du, dass wenn du entsprechende Punkte wie A und A' verbindest, sich alle diese Geraden in einem Punkt treffen. Dem Streckungszentrum (der Punkt, andem die Figur gespiegelt wurde):

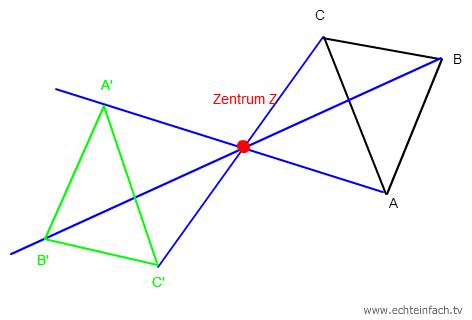
Hier bleiben die entsprechenden Seiten parallel, nicht wie bei der Spiegelung an der Achse. Jedoch ändert sich hier der Umlaufsinn der Beschriftung (jetzt gegen den Uhrzeigersinn).

 

Das sind so die wichtigsten Fakten zu den beiden Spiegelungen, die dir hoffentlich helfen, diese zu unterscheiden...

Ich hoffe, ich konnte helfen und du verstehst es jetzt!

Simon

 

Comments

Für die Funktionen schau bitte beim Mathecoach....

Answer 2

 

Der rote Graph ist hier achsensymmetrisch zur y-Achse. Die Bedingung lautet

f(-x) = f(x)

Der blaue Graph ist punktsymmetrisch zum Koordinatenursprung. Die Bedingung lautet

f(-x) = -f(x)

Comments

Was bedeutet diese Bedingungen im Detail?

---

Die Bedingungen sind nur relevant wenn du Punktsymmetrie und Achsensymmetrie bei Funktionsgraphen untersuchen sollst.

Wenn die Y-Achse die Spiegelachse ist, dann muss z.B. der Funktionswert an der Stelle +3 gleich dem Funktionswert an der Stelle -3 sein. Also f(-x) = f(x)

Wenn man eine Punktsymmetrie untersucht bedeutet es das die Punkte am Koordinatenursprung gespiegelt werden können. Das heißt das der Funktionswert an der Stelle +3 z.B. gleich dem negativen Funktionswert an der Stelle -3 ist. Also f(-x) = -f(x)