Elastizitäten, Definitionsbereich: f(x)=ln(1+x) und h(x)=(1+x^2)^{1/2}

Question

Elastizität: E

Hallo ich habe folgende Aufgabe:

a.  f(x)=ln(1+x) D=(-1, unendlich)

b. h(x)=(1+x^2)^{1/2}  äußere Funktion als Wurzel D=R

Bestimme dabei jeweils auch die Definitinsbereich von E und ( außer im Fall a und b) diejenigen Teilmengen von Definitionsbereich E auf denen E(x)=1 E(x) großer1 bzw. E(x) kleiner 1

 

Könnte mir vielleicht jemand erklären was man genau da machen muss , also wie ist diese aufgabe zu verstehen?

Mein Ansatz war so ,dass ich ich die funktionen abgeleiten habe und in die Elastitätformel eingesetzt  ,also

x* f(x)' /f(x)   , anschließend  wollte ich dann nach x auflösen um den Definitionsbereich von E zu finden

ich bin mir nicht sicher, denn ich habe nicht die volle punktzahl bekommen   .... ich hoffe ihr könnt mir da weiter helfen

 vielen dank erst mal

Answer 1

 

Sind den hier f und h Nachfrage-Preis-Funktionen? Ich nehme an, du weisst das irgendwoher und gibst die richtige Formel für E(x) an.

E(x) = x* f(x)' / f(x)   , anschließend  wollte ich dann nach x auflösen um den Definitionsbereich von E zu finden 

Es ist ja schon ein D für f vorhanden. Das kann für E nur noch weiter eingeschränkt werden. Du musst da sicher aus dem Definitionsbereich ausschliessen, dass f(x) = 0 ist, was bei x=0 der Fall ist.  Also D\{0}

Nach deinem Ansatz:

f(x) = ln(x+1)

f ' (x) = 1/(x+1)

E(x) = x / ((x+1)*ln(x+1))                hat Definitionsbereich (-1,∞) \ {0}      

Hier bist du mit f eigentlich fertig. Der zweite Teil der Fragestellung bezieht sich gar nicht auf f und h.

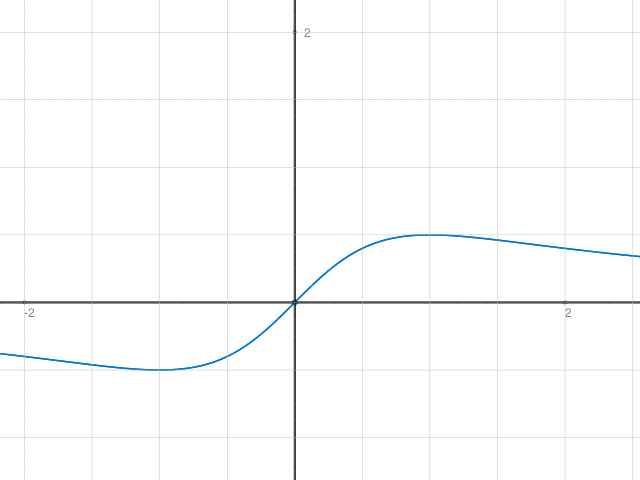
Illustration zum Bisherigen: Im Graphen sieht man die Definitionslücke bei x=0 gar nicht. Grund: Im Zähler steht auch gerade 0. Man kann ablesen, dass die Definitionslücke hebbar wäre. Mit E(0): = 1 ist die Funktion stetig in ganz D. 

 

h(x)=(1+x²)^1/2

h' (x) = 1/2 * 2x / (1+x^2)^{1/2} =  x / (1+x^2)^{1/2}

E(x) = x* f(x)' / f(x)  = x / ((1+x^2)^{1/2} )^2 = x / (1 + x^2)  

Auch hier ist die Division durch 0 auszuschliessen aus dem D der Funktion h.

Da 1+x^2 nie 0 ist, wird der Definitionsbereich nicht eingeschränkt. Er ist ganz R. fertig.

Auch hier zur Illustration der Graph von E(x)