Limes berechnen für: lim(x->0) sin(3x)*cos(5x) / tan(x)

Question

Ich soll den Limis finden und die einzelnen Rechenschritte angeben. 

Die Gleichung sin(3x)*cos(5x) / tan(x) als Funktion sieht so aus: 

Also müsste 3 herauskommen. 

Jedoch wie rechne ich das?

Dankeschön für eure Hilfe!

Answer 1

Du hast erst mal recht, dass 3 rauskommen müsste.

Um das zu berechnen, kannst du hier umformen bis du sozusagen den undefinierten Wert rauskürzen kannst.

 

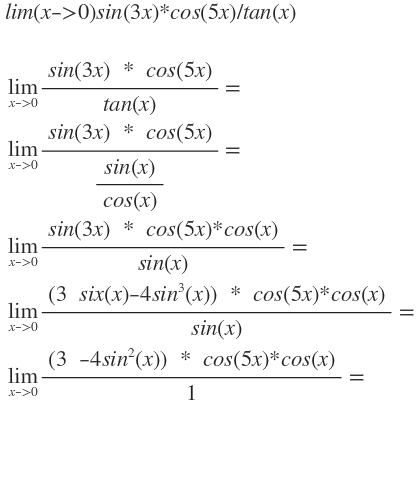
Die Umformung von sin(3x) stammt aus der Dreifachwinkelformel, die eine Folge aus den Additionstheoremen für sin und cos ist.

Kürzen mit sin (x) ist die einzige Nicht-äquivalenzumformung, sie darf strenggenommen nur neben den Nullstellen von sin(x) vorgenommen werden. Bis beliebig nahe zur Definitionslücke.

Nach dem Kürzen kann man 'lim' weglassen und x=0 einsetzen und kommt auf den Schluss der Grenzwertberechnung

= (3 - 4sin²(0))*cos(5*0)*cos(0) = 3*1*1 = 3