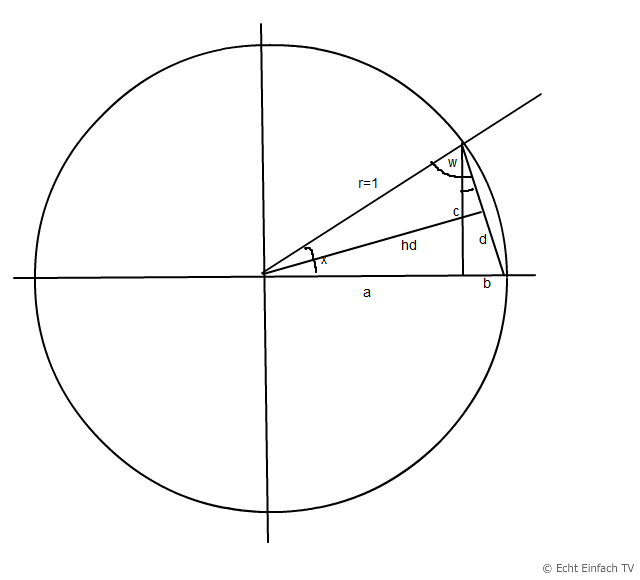
Im Einheitskreis siehst Du, dass b = 1 -cos(x) ist. a entspricht cos(x).
c entspricht dem sin x.
Das Dreieck bcd ist rechtwinklig. Der Winkel y zwischen c und d ist also berechenbar mit tan y = b/c.
b / c ist also (1-cos(x)) / sin(x) und entspricht dem tangens y.
Jetzt musst du nur noch zeigen, dass y = x/2
Das ist so, weil, das Dreieck, gebildet vom Winkel x und d gleichschenklig ist.
w-y ist (90° -x) und w = 90- x/2
90 - x/2 - y = 90 - x -> y = x/2
LG
Capricorn