Hallo
Ich denke ich weiß was Du meinst.
Allgemeine Parabelgleichung:
y=a*(x-b)^2+c
a // streckung, hier a=1 oder a=-1, da es sich um eine Normalparabel handelt
b // Verschiebung in x-Richtung, ist b positiv -> Verschiebung nach rechts, negativ -> links
c // Verschiebung in y-Richtung, hier c=0 da nur eine Verschiebung in x-Richtung erlaubt ist laut Aufgabenstellung
m // wird im Folgenden als Steigung verwendet
zu a)
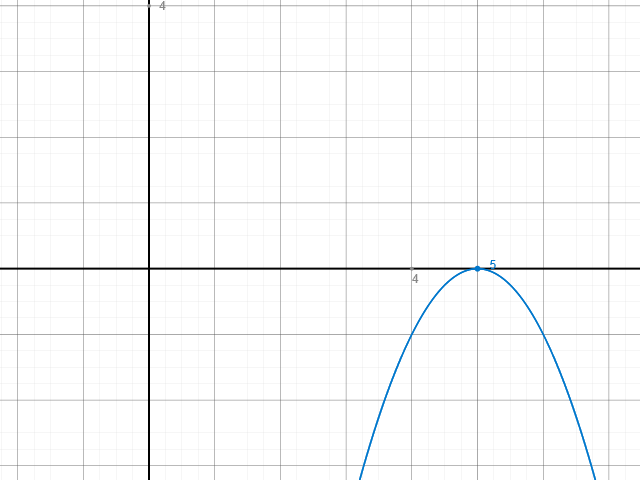
Da gilt m<0 für x>5 und m>0 für x<5 und c=0, liegt der einzige Punkt an dem die Steigung 0 ist bei S(5|0).
Das ist der Scheitelpunkt der Parabel. Daher ist b = 5.
Da die Parabel für x>5 negative Steigung hat:
y'(x)=m=2*a*(x-b), mit x>5, und m<0 gefordert
folgt: 2*a*(x-b)<0; a<0; -> a=-1;
y(x) = -(x-5)^2
zu b)
c=0;
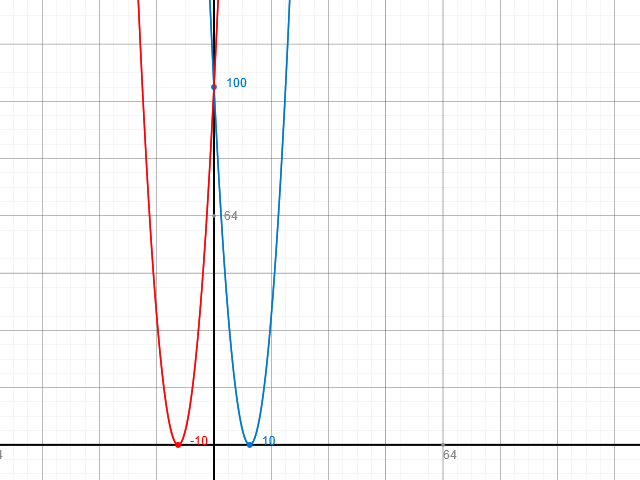
da der Schnittpunkt mit der y-Achse positiv einen positiven Wert hat und der Scheitelpunkt auf der x-Achse liegt, kann a nur noch 1 sein. a=1.
y(x) = (x-b)^2;
y(x=0)= 100; // y an der Stelle x = 0 hat den Wert 100
100 = (0-b)^2;
100 = b^2;
b1 = +sqrt(100) = 10; // Es gibt zwei Lösungen, sqrt = Wurzel
b2 = -sqrt(100) = -10;