Der Basiswechsel / Abbildungsmatrix .

Question

Hi ich habe eine Frage zum Basiswechsel.

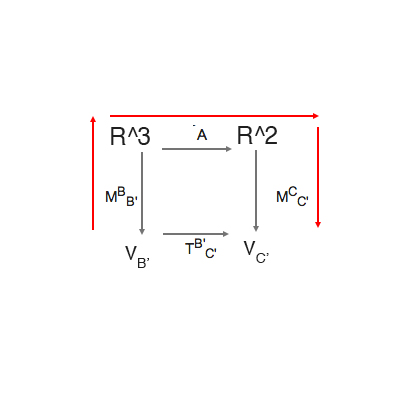
Sei f eine Lineare Abbildung R^3 -> R^2
und die Abbildungsmatrix = A

Sei B' eine von der Standardbasis (B) abweichende Basis von R^3. (Mit b_{1B' ----})
Sei C' eine von der Standardbasis (C) abweichende Basis von R^2.
Nun gibt es ja eine Matrix die Vektoren die unter B geschrieben sind unter B' Darstellen: M^B_B'
Und eine Matrix die Vektoren die unter C geschrieben sind unter C' darstellen: M^C_C'

Gesucht ist also eine Abbildungsmatrix die f mit  B' nach C' Abbildet : T^B'_C'..

Eigentlich müsste ich nun  M^B_B'  ^-1 bestimmen und dann die Matrizen multiplizieren:

 T^B'_C'. =  M^B_B'  ^-1 *  A   *   M^C_C'   und ich bin fertig.

 

Was mir nicht einleuchtet ist, dass man immer wie Folgt vorgeht:

 T^B'_C'..   =    M^C_C'   (   A*(b_1B')   A*(b_2B')​  A*(b_3B')​  ) .

 

Dabei kommen bei mir 2 Unterschiedliche Ergebnisse heraus!

 

 

Comments

Als Beispiel könnte man einmal diese Aufgabe nehmen:

 

 

---

dazu bekomme ich als 

M^B_B' :    {{1, 0, -1}, {2, 1, 0}, {1, 1, -2}}

M^C_C'  :  {{1,2},{-1,2}}     

A :         {{2,-1,1},{9,0,-2}}     

 M^B_B'  ^-1  :  {{2/3, 1/3, -1/3}, {-4/3, 1/3, 2/3}, {-1/3, 1/3, -1/3}}

---

Ich habe leider keine Ahnung, ob das der Fehler ist, der sich eingeschlichen hat, oder ob da sonst etwas nicht stimmt ;)

M^C_C'  :  {{1,3},{-1,2}}    

---

Ich geh das nochmal komplett durch.

Danke schon einmal.

Answer 1

Ein möglicher Fehler liegt im Folgenden:
du musst streng auf die Reihenfolge der Matrizen achten.

 

Du möchtest eine Matrix berechnen, die Vektoren aus ℝ³ nach ℝ² abbildet. Das heißt, die notwendige Reihenfolge ist die folgende:

- Vektor aus B' nach B transformieren
- Abbildung anwenden
- Vektor aus C nach C' transformieren

dabei wirken Matrizen immer auf den Vektor, der rechts von ihnen steht.

Ganz links steht also T^C_C', dann kommt A und anschließend T^B_B'^-1 =: T^B'_B

T^B'_C' = T^C_C' A^B_C T^B'_B