Basis von direkten Summen

Question

Es seien K ein Körper, U und V zwei K-Vektorräume und I und J zwei Mengen.

(u_i)_i∈I  ein System von Vektoren u_i  ∈ U

(v_i)_j∈J  ein System von Vektoren v_j  ∈ V

Man betrachte das System : (w_k)_k∈I∪J   von Vektoren in U ⊕ V mit:

w_k =      | (u_k,0)  falls k ∈ I

|(0,v_k)    falls k ∈ J

Zeigen Sie: Das System (w_k)k∈I∪J  in  U ⊕ V st ein linear unabhängiges System/ein Erzeugendensystem/ 
eine Basis genau dann, wenn die beiden Systeme (u_i)_i∈I  und (v_i)_j∈J die entsprechende 
Eigenschaft bezüglich U respektive V haben.

Answer 1

Lineare Unabhängigkeit:

"=>"

(u_i)_i∈I  ist lin unabh in U => (u_i,0)_i∈I sind lin. unabh.; analog für v    (*)

Σ_i∈I α_i (u_i,0) + Σ_j∈J β_j (0,v_j) = (0_u,0_v)       0_u,0_{v sind Nullvektoren im jeweiligen VR}

_<=> Σ_i∈I  (α_iu_i,0) + Σ_j∈J  (0,β_jv_j) = (0_u,0_v)

=> Σ_i∈I  α_iu_i = 0_{u   und}  Σ_j∈J β_jv_j = 0_{v  wegen (*) folgt} α_i = 0 für alle i ∈ I    und   β_j = 0 für alle j ∈ J.

daraus folgt (w_k)_k∈I∪J  sind linear unabhängig

"<="

Vorausgesetzt ist nun: Lin. ua. von w_j : d.h.

" Σ_k∈I∪J  α_kw_k = 0 => α_k = 0 für alle k aus J und I   "

Aus der Definition von w folgt nun

da für k ∈ I kein Beitrag im rechten Teil erreicht wird folgt aus lin. Uabh. von w_k die lin ua von v_k

da für k ∈ J kein Beitrag im linken Teil erreicht wird folgt aus lin. Uabh. von w_k die lin ua von u_k

--------------------

Erzeugendensystem:

"==>"

Annahme: u_i erzeugen U und v_j erzeugen J

Die Vereinigung von u_i und v_j erzeugt U⊕V wegen der Definition der direkten Summe

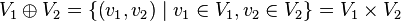
Den mit der Vereinigung erhalten wir alle möglichen Vektoren aus U⊕V (wegen Def. von w).

"<=="

Annahme: w_k erzeugen U⊕V 

dann u_i erzeugen U ,da die v_j keinen Beitrag in U liefern und die w_k  U⊕V  erzeugen

und andersrum analog.

-----------

Basis:

"==>"

Annahme: u_i Basis von U, v_j Basis von V

==> u_i , v_j lin unabh. und erzeugend

bereits bewiesen: ==> w_k sind lin unabh. und erzeugen  U⊕V 

==> w_k bilden Basis von  U⊕V 

"<=="

analog

--

q.e.d