Kleinste Distanz eines Punktes zu einem Quadrat

Question

den kleinsten Abstand eines Punktes zu einem Kreis zu berechnen, ist ja nicht schwer. d = sqrt(x^2 + y^2) - radius (Also x,y = Abstand zum Mittelpunkt des Kreises). Aber wie kann man das für ein Quadrat machen? Dort ist ja der Abstand des Mittelpunktes zu den Kanten unterschiedlich.

Meint ihr man kann dafür eine Formel aufstellen? Irgendwelche Ideen?

 

Danke,

Thilo

Answer 1

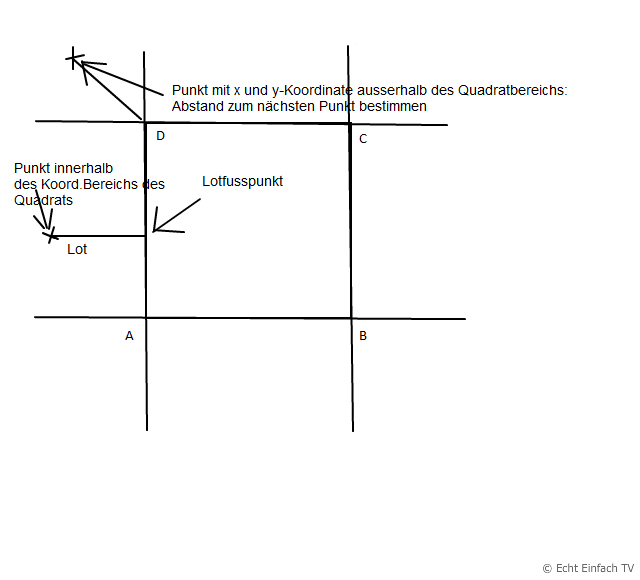
Kann man annehmen, dass die Quadratseiten parallel zu den Koord.-Achsen verlaufen?

Dann ist der kürz. Abstand immer der des Punktes zu einer Ecke des Quadrates, es sei denn, die x- oder y-Koordinate des Punktes befindet sich innerhalb der Grenzen von xA und xB, bzw. yB und yC des Quadrates. Weisst Du was ich meine?

Für den Fall, dass sich der Punkt mit mindestens einer Koordinate (x oder y)  innerhalb des Bereichs des Quadrates befindet, dass muss aber nicht innerhalb des Quadrates sein, kannst Du wie folgt vorgehen:.

Geradengleichung der nächsten Seite bestimmen, Gleichung des Lotes auf diese Gerade durch den Punkt bestimmen, Lotfusspunkt bestimmen, Abstand Lotfusspunkt zum Quadrat ausrechnen.