Nr.1. - Die drei Freunde verlosen Ämtchen... Nr. 2. 20 Kugeln. Schätzung vorhandene Kugeln je Farbe

Question

Hier sind die nächsten Fragen,  wenn es einer kann, was wieso immer der Fall ist ^^ , bei guter Antwort, gibts'n Pluspunkt ;D  danke im voraus

1.) Die drei Freunde Anton, Bert und Conrad zelten gemeinsam. Jeden Morgen losen die drei aus, wer einkaufen geht. Die beiden anderen entscheiden durch ein weiteres Los, wer von ihnen die Mahlzeiten zubereitet.

a.) Zeichnen Sie ein ein Baumdiagramm für diesen zweistufigen Zufallsversuch.

b.) Wie groß ist die Wahrscheinlichkeit, dass Anton einkauft und gleichzeig Bert für die Mahlzeiten verantwortlich ist?

c.) Wie groß ist die Wahrscheinlichkeit, dass Conrad sich um nichts kümmern muss?

 

2.) In einem Gefäß befinden sich 20 Kugeln. Sie unterscheiden sich nur durch die Farbe. Sie sind entweder grün oder rot oder blau. Aus diesem Gefäß wird zufällig eine Kugel entnommen und anschließend wieder zurückgelegt. Dieser Vorgang wird mehrfach ausgeführt. Die Tabelle zeigt, wie oft dabei grüne, blaue bzw. rote Kugeln gezogen wurden.

Grüne Kugeln                   Blaue Kugeln                                               Rote Kugeln                                                                                                                                
 
 6                                          12                                                                     22

a.) Berechnen Sie die relativen Häufigkeiten für das Ziehen von grünen Kugeln und für das Ziehen von blauen Kugeln.

b.) Geben Sie aufgrund der Berechnungen in a.) eine Vermutung für die Anzahl der im Gefäß enthaltenen grünen, blauen, und roten Kugeln an.

c.) Geben Sie an, wie man durch Zufallsversuche die Sicherheit der in b.) gewonnenen Vermutung erhöhen kann.

d.) Die in a.) berechneten relativen Häufigkeiten sollen bei dem oben beschriebenen Zufallsversuch ,,Ziehen einer Kugel mit anschließendem Zurücklegen" als Wahrscheinlichkeiten gelten. Wie groß ist die Wahrscheinlichkeit, dass beim zweimaligen Ausführen des Versuchs eine grüne und eine blaue Kugel gezogen wird?

Answer 1

1.

a) zeichnen Sie ein Baumdiagramm für diesen zweistufigen Zufallseversuch

 

------------------------------------------------------------------------------------------------------------------------------------------------------------

 

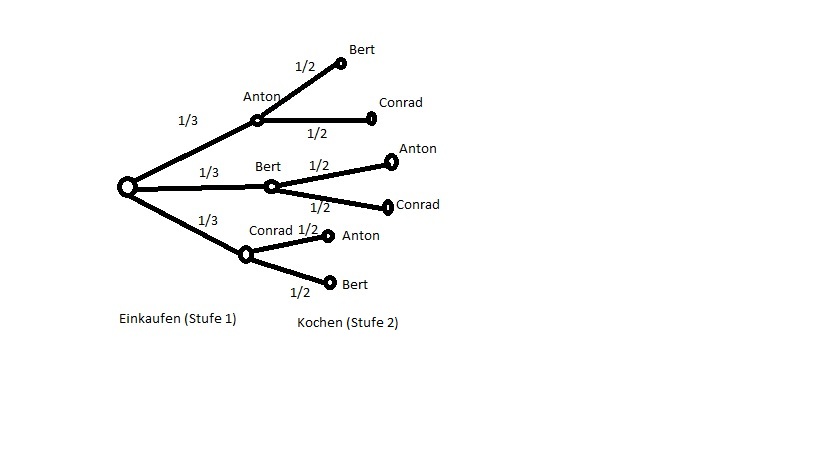
b)

Laut der Multiplikationsregel gilt:

Die Wahrscheinlichkeiten der Stufen (Einkaufen, Kochen) werden miteinander multipliziert um die Gesamtwahrscheinlichkeit für dieses Ereignis (Anton einkaufen, Bert kochen) zu erhalten

1/3*1/2=1/6

 

Laut der Additionsregel gilt:

Addiert man alle Gesamtwahrscheinlichkeiten (Für jeden Verlauf) erhält man die Wahrscheinlichkeit 100% (oder in Dezimalzahlen 1)

 

Also musst du entweder alle Gesamtwahrscheinlichkeiten addieren bei denen Conrad nichts machen muss, oder du rechnets 100% minus aller Verläufe in denen er entweder einkaufen oder kochen muss

Also:

1/6+1/6=2/6=1/3 (gekürzter Bruch)

oder

1-1/6-1/6-1/6-1/6=2/6=1/3 (gekürzter Bruch)

------------------------------------------------------------------------------------------------------------------------------------------------------------

2.

a) Um die relative Häufigkeit zu berechnen teilst du die absolute Häufigkeit (in diesem Fall ist die absolute Häufigkeit von grünen Kugeln 6 und von blauen Kugeln 12) durch die Anzahl der gesamten Anzahl an gezogenen Kugeln (in diesem Fall 6(grüne)+12(blaue)+22(rote)=40)

In Formeln (falls nötig):

E= Ereignis (bsp. grüne Kugel wurde gezogen)

H(E)= Absolute Häufigkeit

h(E)= Relative Häufigkeit

n= Gesamt Anzahl der Stichprobe

=>h(E)=H(E)/n

 

Also:

relative Häufigkeit das eine grüne Kugel gezogen wurde 6/40=0,15

relative Häufigkeit das eine blaue Kugel gezogen wurde 12/40=0,3

--------------------------------------------------------------------------------------------------------------------------------------

b)

Es ist wahrscheinlich das am meisten rote Kugeln und am wenigsten  grüne Kugeln in dem Gefäß sind, da die relative Häufigkeit eine grüne Kugel zu ziehen geringer ist als die, einer blaue Kugel zu ziehen. Ebenso wird es sich für die relative Häufigkeit für blaue Kugeln im vergleich zu roten Kugeln verhlaten.

 

---------------------------------------------------------------------------------------------------------------------------------------------------------

c)

Bei dieser Aufgabe kann ich nur vermuten:

Ich schätze die wollen das du die Stichprobe, also die Anzahl der Ziehungen der Bälle vergrößerst. Anstatt 40 mal ziehen vielleicht 70, 80, 90 mal ziehen. Je größer die Stichprobe desto aussagekräftiger ist der Versuch.

------------------------------------------------------------------------------------------------------------------------------------------------------------

d)

Hier tritt wieder die Multiplikationsregel und die Additionsregel in Kraft.

Die relative Häufigkeit aus a) ist also jetzt die allg. Wahrscheinlichkeit.

Wie bei Aufgabe 1 haben wir hier 2 Stufen, also rechnest du 0,15*0,3=0,045 (4,5%).

Dies galt jetzt für den Fall das wir erst eine grüne und dann eine blaue ziehen.

Da in der Aufgabe keine genaue Reihenfolge steht (also erst grün dann blau oder anersrum) müssen wir beide Fälle berücksichtigen.

Es kann also auch passieren das wir erst eine blaue ziehen und dann eine grüne.

das Ergebnis wird das gleiche sein 0,3*0,15=0,045(4,5%).

Da diese aber als 2 mögliche Verläufe betrachtet werden müssen, müssen wir jetzt beide Verläufe, laut der Additionsregel addieren, damit wir die gesamte Wahrscheinlichkeit haben.

0,045+0,045=0,09(9%).

Die Wahrscheinlichkeit eine grüne und eine blaue Kugel zu ziehen, wenn man 2 mal reingrieft liegt also bei 9% (oder 0,09 als Dezimalzahl)

 

Ich hoffe ich konnte dir helfen.

Ich bin hier bisher noch nicht angemeldet, bin aber stark am überlegen, da ich studiere und Mathelehrer werden will.

Wenn ich dir also helfen konnte, lass es mich wissen. Dann werde ich mich wahrscheinlich hier anmelden und auch in Zukunft weiterhelfen.

Comments

Ich bin zwar nicht der Fragesteller, aber ich würde dich ermutigen, wiederzukommen und weiterhin zu helfen.

Deine Antwort ist sehr schön und ausführlich!

---

ich kann zwar nichts versprechen, neue Fragen zu stellen aber sobald ich was habe, melde ich mich hier ;)

---

Das bezog sich natürlich auch auf andere, die eine Frage haben ;-)

---

achso, sag das doch gleich, dann melde ich mich nicht mehr ;D nee spaß