Umkehr- Modellbildungsaufgaben: Eine Firma bringt ein völlig neuartiges Sportgerät auf den Markt.

Question

 sorry für die vielen Fragen, aber ich brauch diese Frage , welche auch meine letzte sein wird für heute(hoff ich mal :p)

Ich verlange jetzt etwas zu viel von euch aber bitte kann jemand diese Aufgabe wirklich detalliert rechnen.

Es tut mir leid, dass ich so viele sachen verlange und frage aber bitte helft mir.

 

Aufgabe:

Eine Firma bringt ein völlig neuartiges Sportgerät auf den Markt. Zum Zeitpunkt t=0 (minimum) besitzen es 0% der Bevölkerung, nach 3 Monaten 1. Nach 8 Monaten verlangsamt sich das Wachstum (Tipp: Wendepunkt). Nach 16 Monaten wird der Höhepunkt erreicht.

-Stelle den Zusammenhang zwischen Prozentsatz in der Bevölkerung durch eine geeignete Polynomenfunktion dar. Runde die Koeffizinenten auf 4 Dezimalstelllen.

- Wie viel Prozent der Bevölkerung besitzen maximal das Sportgerät?

 

Meine Ideen: Sry Leute aber ich weiß nicht mal wie ich anfangen soll :S

vielleicht bei 8 monaten = wendepunkt also 2. Ableitung.

 

Lösung aus lösungsbuch: Polynomenfunktion 4. Grades, der erste Koeffizient wird jedoch verschwindend klein und wirkt sich im betrachteten Bereich nicht auf den Kurvenverlauf aus.

f(x)= -0,00053x^3 + 0,1270x^2

maxilaml ca. 11% der Bevölkerung

 

Danke auch wenn ihr sie nicht löst

 

MfG

Answer 1

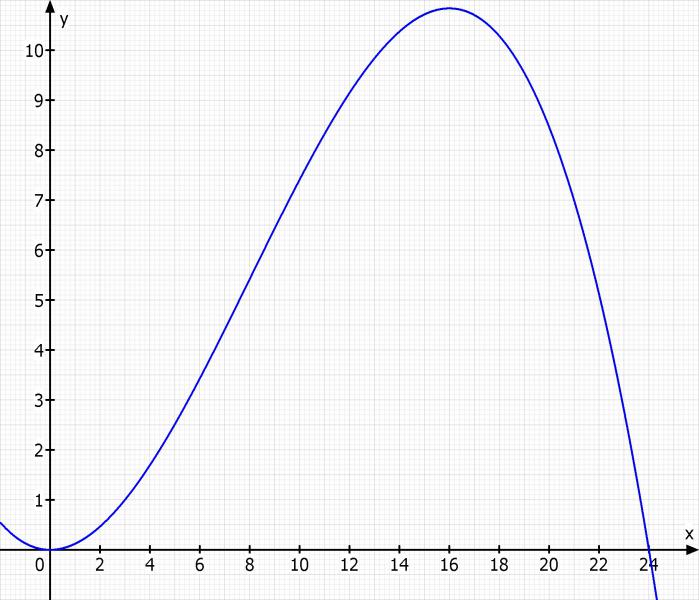
Eine Firma bringt ein völlig neuartiges Sportgerät auf den Markt. Zum Zeitpunkt x=0 (minimum) besitzen es 0% der Bevölkerung, 

f(0) = 0
f'(0) = 0

nach 3 Monaten 1%.

f(3) = 1

Nach 8 Monaten verlangsamt sich das Wachstum (Tipp: Wendepunkt).

f''(8) = 0

Nach 16 Monaten wird der Höhepunkt erreicht.

f'(16) = 0

Wir haben 5 Bedingungen und damit eine Funktion 4. Grades

f(x) = ax^4 + bx^3 + cx^2 + dx + e
f'(x) = 4·a·x^3 + 3·b·x^2 + 2·c·x + d
f''(x) = 12·a·x^2 + 6·b·x + 2·c

 

f(0) = 0
e = 0

f'(0) = 0
d=0

f(3) = 1
81·a + 27·b + 9·c = 1

f''(8) = 0
768·a + 48·b + 2·c = 0

f'(16) = 0
16384·a + 768·b + 32·c = 0

Die Lösung des LGS lautet a = 0 ∧ b = - 1/189 ∧ c = 8/63

f(x) = - 1/189 x^3 + 8/63 x^2

Skizze:

Comments

Die Fragen jetzt zu beantworten solltest du selber schaffen.

Wenn du noch Probleme hast melde dich einfach.

---

Ok danke schonmal. Falls ich was nicht verstehe melde ich mich EDIT: wieso setzt du f(0) auch in die erste ableitung?

---

Kannst du auch kurz mir noch bitte kurz sagen warum du bei t=0

bei f(0)=0 und f ' (0)=0 einsetzt und nicht nur bei f(0)=0

Also warum auch in die Erste Ableitung?

 

Danke für deine hilfe

---

Weil am Zeitpunkt 0 auch ein Minimum sein sollte und damit die Ableitung 0 sein muss.