Cäsium 137: HWZ von 30,17 Jahren
Also
x30,17 = 0,5 | auf beiden Seiten die 30,17. Wurzel ziehen liefert x:
x ≈ 0,9772871932
Probe:
0,977287193230,17 = 0,5
a) Nach wie vielen Jahren ist die Cäsiumbelastung auf 25 % bzw. 12,5 % bzw. 11% gesunken?
0,9772871932x = 0,25 | klar, dass es nach 60,34 Jahren sein muss: 0,5 * 0,5 = 0,25 = 25%
Man kann aber auch rechnen
ln(0,25)/ln(0,9772871932) ≈ 60,34
Nach 60,34 Jahren ist die Belastung auf 25% gesunken.
0,9772871932x = 0,125 | natürlich nach 90,51 Jahren: 0,5 * 0,5 * 0,5 = 0,125 = 12,5%
Aber auch hier:
ln(0,125)/ln(0,9772871932) ≈ 90,51
Nach 90,51 Jahren ist die Belastung auf 12,5% gesunken.
Bei 11% sehen wir die Lösung nicht auf Anhieb:
ln(0,11)/ln(0,9772871932) ≈ 96,07
Nach ca. 96,07 Jahren ist die Belastung auf 11% gesunken.
B) Zeichne den Graph des radioaktiven Zerfalls von Cäsium und lies ab ,wann 20 ,5,2, % vorhanden sind ,gib die Jahreszahlen an
Man kann sich eine Wertetabelle nach obigem Verfahren aufstellen und dann den Graphen zeichnen.
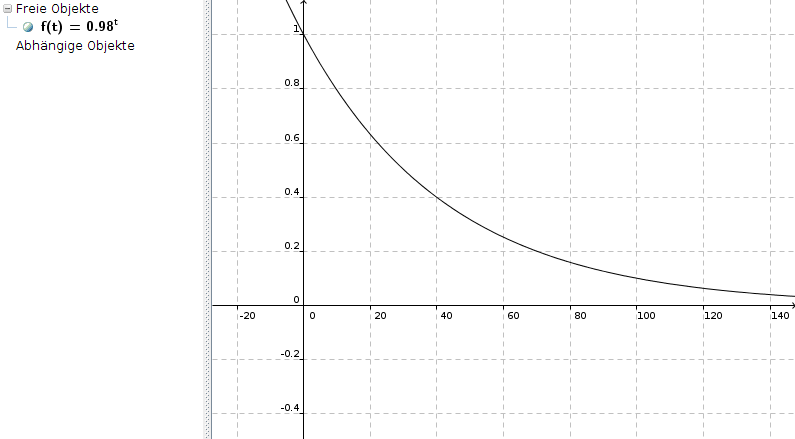
Oder man gibt in eine Graphikplotter die Funktion
f(t) = 0,9772871932t ein und erhält dann so etwas (beachte die unterschiedliche Skalierung der x- und y-Achse):
Besten Gruß