Fläche zwischen den Graphen von f-9, der x-Achse und der Geraden zu y=4

Question

Ich habe folgende Funktionenschar

$$f(x,k)={ x }^{ 2 }+2*k+\frac { { k }^{ 2 } }{ { x }^{ 2 } } $$

Nun die Aufgabe:

Fläche zwischen den Graphen von f(x,-9), der x-Achse und der Geraden zu y=4:

f(x,-9) ist ja

$$f(x,k)={ x }^{ 2 }+\frac { 81 }{ { x }^{ 2 } } -18$$

und y=4

Nun habe ich dies gezeichnet und die Fläche, die ich bestimmen soll schraffiert. Dies sieht so aus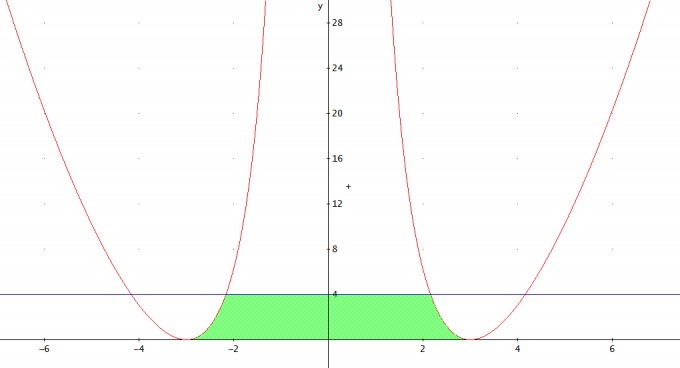

Das Grüne, ist die Fläche, die ich berechnen muss. Nun habe ich so gedacht:

Ich habe die INtegrationsgrenzen, also -3 und 3 (Die NST) ausgerechnet und dann einfach das Integral von f(x,-9)-4 ausgerechnet

Es kam dann dieses Ergebnis raus:

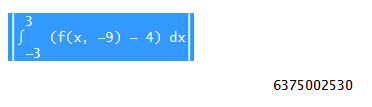
Ist das alles richtig gerechnet? Weil mir kommt diese Zahl extrem hoch vor.. Habe ich alles richtig gemacht?

ICh würde mich über Antworten freuen.

Answer 1

Du darfst nicht über Pole integrieren.

Wähle die Grenzen 2 und 3, wenn du f_(-9) integrierst.

Verdopple das Ergebnis und addiere die Rechtecksfläche 4*4 = 16.

Comments

EDIT: 2 ist geschätzt.

Genau bekommst du die Grenze, wenn du 4 = f(x, -9) nach x auflöst.

---

Was meinst du genau mit"Du darfst nicht über Pole integrieren"?

---

Deine Funktion hat bei x=0 einen sogenannten Pol (= vertikale Asymptote). Da kann's bei der Integration Probleme geben, wenn du das Integral nicht bei x=0 unterteilst.

---

Auch wenn ich das so mache, kommte ich auf das gleich Ergebnis (Ich benutze DERIVE)

---

Jetzt aber nochmals zu deiner Skizze.

Da interessiert dich doch die grüne Fläche.

Die Funktionsgleichung f(x, -9) gilt nur ungefähr zwischen 2 und 3, sowie zwischen -3 und -2.

zwischen etwa -2 und 2 gilt y=4. Halte dich da an meine oder georgborns Anweisungen in den Antworten.

---

Ich habe es nun verstanden. Der Fehler war, dass ich trotzdem noch beide Funktionen bei der Rechnung benutzt habe

nochmals

Answer 2

Für die rechte Seite ( 1.Quadrant )
Du bestimmts den Schnittpunkt  f  und y = 4
x = 2.162

Die Stammfunktion ist
s ( x ) = ∫ x^2 + 2* (-9) + k^2 / x^2 dx

Die grüne Fläche ist
[ s ( x ) ] _2.162 ³ + 4 * 2.162 ( Rechteck )

Bei Fragen wieder melden.

mfg Georg