bei einer Übungsaufgabe komme ich bei der Teilaufgabe nicht zurecht.
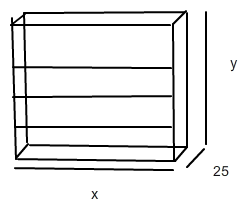
Ikea möchte ein Regal mit den Maßen 80/100/25 (B/H/T in cm) so ändern, dass das Volumen bei gleichem Materialverbrauch maximal wird.
Es gibt 2 vertikale Leisten und insgesamt 5 horizontale Leisten
Wie muss die Breite x und die Höhe y gewählt werden?
Hab ich schon gelöst :
Vmax: x*y*25
Oberfläche: 5*(25x)+ 2*(25y)
--> 125x + 50y= 15000cm²
NB nach y umgestellt : (300 - 2,5x)=y
in HB: V(x)=7500x-62,5x²
V'(x)=-125x+7500 = 0
x=60 y = 150
Bei dem zweiten Teil komme ich allerdings nicht weiter :
Welche Optimalmaße ergeben sich, wenn die beiden vertikalen Bretter verstärkt werden und daher pro Längeneinheit doppelt so teuer sind wie die horizontalen Bretter ?
Heisst das y soll minimal werden?