Sei K ein Körper und A=((1,1),(0,-1)), B=((1,0),(0,-1)) zwei Matrizen. Gelten folgende Aussagen:?

Question

Sei K ein Körper und seien A,B element von M2(K) gegeben durch

A=   1   1

       0    -1                 und  B=      1   0

                                                    0  -1

 

1. Wenn K=R, sind A und B ähnlich?

2. Wenn K=F2={0;1}, sind A und B ähnlich?

 

Ich bitte um Lösung und bitte mit erklärung

Answer 1

Zwei Matrizen sind ähnlich, falls es eine invertierbare Matrix P gibt mit B=PAP^-1.

1. Hier darfst du als Einträge alle reellen Zahlen wählen, du musst also eine Matrix P finden, die die obige Eigenschaft erfüllt:

Es gilt

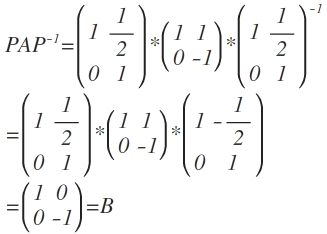
PA{ P }^{ -1 }=\begin{pmatrix} 1 & \frac { 1 }{ 2 }  \\ 0 & 1 \end{pmatrix}*\begin{pmatrix} 1 & 1 \\ 0 & -1 \end{pmatrix}*{ \begin{pmatrix} 1 & \frac { 1 }{ 2 }  \\ 0 & 1 \end{pmatrix} }^{ -1 }\\ =\begin{pmatrix} 1 & \frac { 1 }{ 2 }  \\ 0 & 1 \end{pmatrix}*\begin{pmatrix} 1 & 1 \\ 0 & -1 \end{pmatrix}*{ \begin{pmatrix} 1 & -\frac { 1 }{ 2 }  \\ 0 & 1 \end{pmatrix} }\\ =\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}=B

Also sind A und B ähnlich, wenn K=IR.

 

2. Wenn K=F2={0;1}, dürfen die Einträge der Matrix P nur aus 0 und 1 bestehen. Hierbei gibt es keine Matrix P, die die Gleichung B=PAP^-1 erfüllt (das kannst du einfach ausprobieren, so viele Möglichkeiten gibt es da nicht, wie P aussieht). A und B sind also nicht ähnlich, wenn K=F2={0;1}.