Aufgabe:
7.1.0 Über einen Fluss soll eine Brücke gebaut werden. Der Verlauf der beiden Uferlinien kann durch die Graphen zweier Funktionen abgebildet werden. Das obere Flussufer wird durch die Funktion \( \mathrm{f}_{1} \) mit der Gleichung
\( f_{1}(x)=-\frac{1}{2} x^{4}+2 x^{3}-2 x^{2}+1 \text { und } D_{f_{1}}=R \)
beschrieben.
Das untere Flussufer verläuft wie der Graph der ganzrationalen Funktion \( f_{2} \) dritten Grades mit den Extrempunkten \( \mathrm{H}\left(0 ; \frac{1}{2}\right) \) und \( \mathrm{T}(1 ; 0) \).
7.1.1 Weisen Sie rechnerisch nach, dass für die Funktion \( \mathrm{f}_{2} \) folgende Gleichung gilt:
\( f_{2}(x)=x^{3}-\frac{3}{2} x^{2}+\frac{1}{2} \)
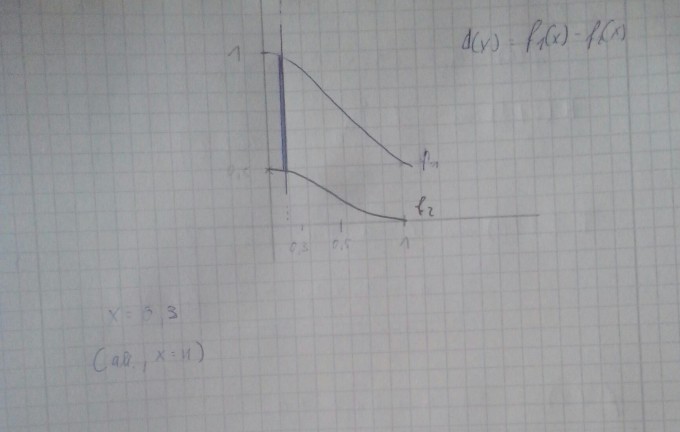
7.1.2 Skizzieren Sie die Graphen der Funktionen \( f_{1} \) und \( f_{2} \) im Intervall \( [0 ; 1] \) sowie den möglichen Brückenverlauf mittels einer Geraden \( \mathrm{x}=\mathrm{u} \) für den Sonderfall \( \mathrm{u}=0,3 \) in ein geeignetes Koordinatensystem.
7.1.3 Ermitteln Sie rechnerisch die Stelle des kleinsten Uferabstandes für den Bau der Brücke und geben Sie den minimalen Abstand d in Meter an. Es gilt: \( 1 \mathrm{LE}=100 \mathrm{~m} \)
Auf die Uberprüfung der Randwerte wird verzichtet.
7.2.0. Die Brücke soll durch Lampen beleuchtet werden, die die Form eines regelmäßigen dreiseitigen Prismas mit der Grundkante a und der Höhe h besitzen. Die Lampen werden mit einer Seite der Mantelfläche an Pfeilern befestigt, so dass für diese Seite kein Material benötigt wird. Das Volumen einer Lampe muss 15 Liter betragen.
7.2.1 Weisen Sie nach, dass die Funktion \( \mathrm{A}_{0} \) mit der Gleichung
\( A_{0}(a)=\frac{\sqrt{3}}{2} a^{2}+\frac{120}{\sqrt{3}} a^{-1} \)
eine Zielfunktion für die Berechnung des Oberflächeninhalts einer dieser Lampen ist.
7.2.2 Berechnen Sie a so, dass der Materialverbrauch minimal wird. Geben Sie die Hohe \( \mathrm{h} \) und den kleinstmöglichen Oberflächeninhalt \( \mathrm{A}_{0} \) in geeigneten Maßeinheiten an.
Ansatz/Problem:
Bei der Aufgabe 7.1.3 komm ich nicht weiter. Meine Lösung von 7.1.1 und 7.1.2 sind nachstehend: