Hallo,
Willkommen in der Mathelounge!
Fasse die Streckenlast pro 'Balken' zu einer Kraft \(F_{L1}\) und \(F_{L2}\) zusammen. Der Angriffspunkt der Kräfte liegt \(x_1\) bzw. \(x_2\) von der Brückenmitte entfernt. Falls Du nicht weißt, wie das geht, so melde Dich bitte
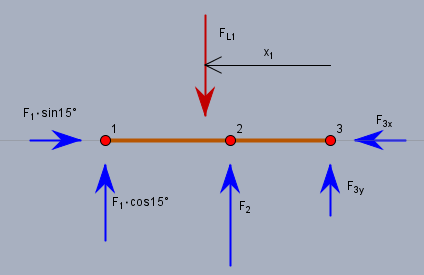
Stelle nun für den linken Teil die Summe aller Kräfte in X- und Y-Richtung auf (horizontal und vertikal), sowie die Summe der Momente um das Lager \(1\):$$\sum F_y: \quad F_1\cos(15°) + F_2 + F_{3y} = F_{L1} \\\sum F_x: \quad F_1\sin(15°) - F_{3x} = 0 \\\sum M_1: \quad 50F_2 + 90F_{3y} = (90-x_1)F_{L1}$$Das gleiche mache für den rechten Brückenteil und die Summe der Momente um das Auflager \(5\) (rechts außen)$$\sum F_y: \quad -F_{3y} + F_4 + F_5\cos(15°) = F_{L2} \\\sum F_x: \quad F_{3x} - F_5\sin(15°) = 0 \\\sum M_5: \quad 90F_{3y} - 50F_4 = -(90-x_2)F_{L2}$$Wegen der Symmetrie ist sicher \(x_1=x_2\) und \(F_{L1}= F_{L2}\).
Löse dann das lineare Gleichungssystem. Auf Grund der Symmetrie muss für \(F_{3y}\) der Wert \(0\) heraus kommen! Und weiter muss deswegen \(F_1=F_5\) und \(F_2=F_4\) sein. Wenn man das im Vorfeld benutzt (benutzen darf), kann man obiges LGS natürlich auch vereinfachen.
Falls etwas unklar ist, so frage bitte nach.
Gruß Werner