Aufgabe:
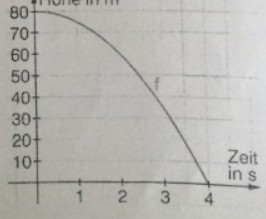
Der freie Fall eines Steins aus \( 80 \mathrm{~m} \) Höhe wird durch die Funktionsgleichung \( f(t)=80-5 t^{2}(t \) in sec. und \( f(t) \) in \( m \) ) modelliert.
a) Berechne, nach welcher Zeit der Stein auf der Erde aufschlägt.
b) Bestimme die Durchschnittsgeschwindigkeit im Intervall \( [0 ; 4] \).
c) In welcher Höhe befindet sich der Stein nach \( 1 \mathrm{~s}, 2 \mathrm{~s} \) und \( 3 \mathrm{~s} \) ?
d) Mit welcher Geschwindigkeit schlägt der Stein auf der Erdoberfläche auf?