Berechnung des Parameters Integralrechnung

Question

kann mir jemand die folgende Aufgabe erklären, weil ich nicht weis was ich machen soll.

LG Thomas

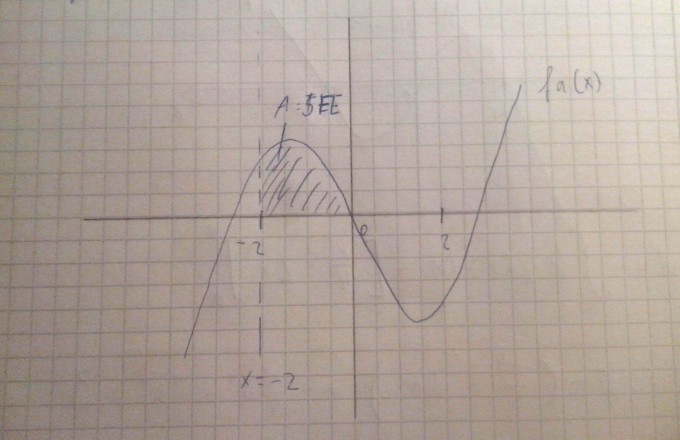
Aufgabe: Berechnung des Parameters a in fa(x), so dass Fläche unter der Kurve im 2. Quadranten zwischen [-2;0] ohne "übergehen" der Nullstelle gleich 5 FE ist.

Skizze dazu:

Answer 1

$$$$möglicherweise soll die Funktion von der Form $f_a(x)=x^3-ax$ mit passendem $a>0$ sein. Dann ist$$5=\int_{-2}^0f_a(x)\,\mathbb dx=\left.\frac14x^4-\frac12ax^2\right\vert_{-2}^0=2a-4,$$woraus $a=\frac92$ folgt. Für dieses $a$ ist wie man leicht nachrechnet auch die Zusatzbedingung erfüllt, denn die zugehörige Funktion weist innerhalb des fraglichen Intervalls keine Nullstellen auf.

Comments

Erklär mir mal wie du auf 1/4x⁴-1/2ax² kommst !?

---

Das ist eine Stammfunktion von $f_a(x)$.

---

Achso ja stimmt auch wieder. Noch eine Frage wie kommt man auf a=9/2?

---

Besagte Fläche berechnet sich in Abhängigkeit des Parameters $a$ wie oben gezeigt zu $A=2a-4$. Lt. Fragestellung soll $A=5$ gelten, also $2a-4=5$. Daraus folgt $a=\frac92$.

---

Ok, alles klar

Danke dir vielmals!