Flächeninhalt (Rechteck) in Dreieck optimieren?

Question

Es ist ein rechtwinkliges Dreieck geben, Seitenlängen bekannt.

Dort drinnen ist ein Rechteck schraffiert. Wie maximiere ich den Flächeninhalt?

Ich will keine Lösung, ich möchte nur wissen, wie man es macht.

Answer 1

Beispiel:

rechtwinkliges Dreieck , Kathete x = 80  / Kathete y = 100

Bedingung →  A = x  * y    , maximal, Nebenbed.  80/100= y /( 100 - x)

A (x) = (80/100) *  ( 100x - x²)  , 80/100 ist konst. Faktor → entfällt also !

A (x) =x² + 100x → Ableitung  A´ = -2x + 100

A´ =0  ,   - 2x+100 =0   ---> x = 50

y  = 80 / 100  *  ( 100 - 50 )  = 4/5 * 50  =  40 !!

Ergebnisse : 40 , 50 .

Answer 2

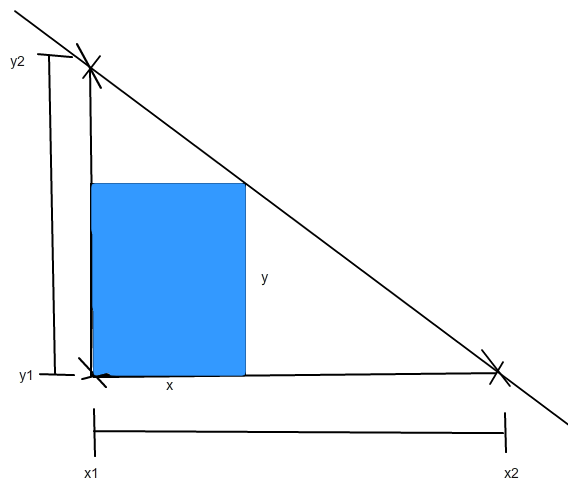
Stell dir das Dreieck als Lineare Funktion vor.

Demnach ist die Funktion y= mx+b

Nun setzen wir mal Punkte ein: x1= 0 x2= 80  y1=0 y2= 50

P(0|80) P2(0|50)

Mit dem Differenzenquotient ist die Steigung also -80/50

Die Nebenbedingung ist also f(x) = -80/50 * x + 50 

Die Hauptbedingung ist der Flächeninhalt des Rechtecks, das am größten werden soll: 

A= x * y Die Y-Koordinate, die die Hypotenuse schneidet ist der höchste Punkt, der möglich ist.

Also A = x* -80/50 * x + 50 

Danach die Ableitung bilden und die anderen Schritte weißt du sicherlich schon ;D

Gruß Luis