Hier eine Skizze
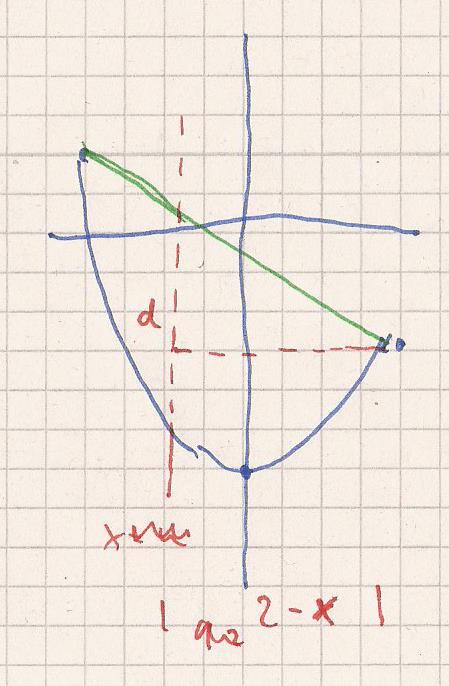
Die Differenzfunktion ist
d = -1/2 * x - ( -1/8*x^3 + 3/4*x^2 - 3)
d = -1/2 * x + 1/8*x^3 - 3/4*x^2 + 3
und entspricht der Gundseite des Dreiecks
Die Höhe des ( Abstand Grundseite zu x = 2 )
h = 2 - x
Die Fläche
F ( x ) = d * h * 1/2
F ( x ) = ( 1/8*x^3 - 3/4*x^2 - 1/2 * x + 3 ) * ( 2 - x ) * 1/2
F ( x ) = -x^4/16 + x^3/2 - x^2/2 - 2*x + 3
F ´ ( x ) = -x^3/4 + 3*x^2/2 - x - 2
Die Gleichung ist algebraisch nicht zu lösen.
Nun ist uns die Lösung ja schon vorgegeben ( x oder u ) = 2 - 2 * √ 2
Eine Extrempunkt wäre wenn F `( 2 - 2 * √ 2 ) = 0 ist
~plot~ -x^3/4 + 3*x^2/2 - x - 2 ~plot~
x = -0.828
Sieht so aus.
Die Steigung wechselt von positiv nach negativ.
Der Punkt ist ein Hochpunkt.
mfg Georg