Aufgabe:
Mein Problem liegt darin, wie ich nicht weiß, was ich mit dem Punkt A anfangen soll. Ich weiß wie das geht ohne einen Punkt im anderen Quadranten. Ich bin gerade schon am verzweifel, weil ich nicht weiß wie ich das angehen soll.
Wäre nett, wenn mit jemand helfen kann :)
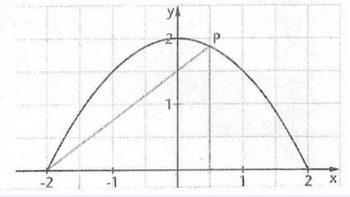
\( \mathrm{P}\left(\mathrm{x}_{\mathrm{p}} | \mathrm{y}_{\mathrm{n}}\right) \) sei ein beliebiger Punkt des Graphen der Funktion \( \mathrm{f} \) mit \( \mathrm{f}(\mathrm{x})=-\frac{1}{2} \mathrm{x}^{2}+2 \)
der oberhalb der x-Achse liegt. Die Parallele zur y-Achse durch den Punkt P, die \( x \) -Achse und die Gerade, die durch \( A(-2 | 0) \) und \( P \) verläuft, bestimmen ein Dreieck. Für welche Lage des Punktes P ist der Flächeninhalt des Dreiecks maximal?
Gesucht ist der maximale Flächeninhalt, deshalb wird ein Funktionsterm zur Berechnung des Flächeninhalts aufgestellt.