Wegen \( 2 \cos( kx) = e^{ ikx } + e^{ -ikx} \) folgt $$ 2 \sum_{k=0}^n \cos(kx) = \sum_{k=0}^n \left( e^{ ikx } + e^{ -ikx} \right) $$
und daraus
$$ \sum_{k=0}^n \left( e^{ ikx } + e^{ -ikx} \right) = \frac{ e^{ i(k+1)x } - 1 }{ e^{ix} -1 } + \frac{ e^{-i(k+1)x} -1 }{ e^{-ix} - 1 } = \frac{ \sin \left[ \left( n+\frac{1}{2} \right) x \right] }{ \sin \left( \frac{x}{2} \right) } + 1 $$ und damit die Behauptung (a)
Zu (b)
Einfach die Fourierkoeffizienten ausrechnen ergibt
$$ a_0 = \frac{8}{3} \pi^2 $$ und $$ a_k = \frac{ 4 }{ k^2 } (-1)^k $$ und
$$ b_k = \frac{ 4 \pi }{ k } (-1)^k $$
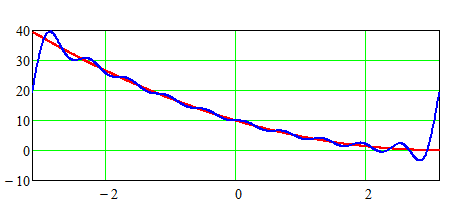
Die Approxiamtion sieht dann für \( n = 10 \) so aus