Punkte P1 und P2 bestimmen die Gerade g1 - Berechne den Schnittpunkt mit Gerade g2!

Question

Die Punkte P1 (1/2) und P2 (3/5) bestimmen die Gerade g1. Die Gerade g2 ist durch y= 5,5- x definiert.

a) Berechne den Schnittpunkt S von g1 und g2.

b) Prüfe die Lösung zeichnerisch.

Answer 1

Du musst hier erstmal die Funktionsgleichungen der beiden Geraden herausfinden. Beziehungsweise eigentlich nur die erste, denn die zweite steht ja schon da:

g₂(x) = 5.5 - x

 

Für g₁ muss ein lineares Gleichungssystem aufgestellt werden.

Die allgemeine Form einer linearen Funktion lautet g₁(x) = mx + n

Bekannt ist, dass die beiden Punkte P₁ und P₂ auf dem Graphen liegen, also muss gelten:

g₁(1) = 2

g₁(3) = 5

Das liefert die beiden Gleichungen:

m*1 + n = 2 (I)

m*3 + n = 5 (II)

Zieht man die erste Gleichung von der zweiten ab, so erhält man:

m*3+n - (m*1+n) = 5-2

2m = 3  | :2

m = 1.5

Eingesetzt in Gleichung (I) ergibt sich:

1.5*1 + n = 2  | -1.5

n = 0.5

 

Die Funktionsgleichung lautet also: g₁(x) = 1.5x + 0.5

a) Um nun den Schnittpunkt zu bestimmen, muss g₁(x)=g₂(x) gelten:

1.5x + 0.5 = 5.5 - x  | +x

2.5x + 0.5 = 5.5  | -0.5

2.5x = 5  | :2.5

x = 2

 

Eingesetzt in eine der beiden Gleichungen erhält man dann den Punkt (2, 3.5) als Schnittpunkt.

 

b) Für die zeichnerische Lösung müssen die beiden Funktionen natürlich gezeichnet werden (das ist schwer vorzumachen, deswegen einfach nur das Bild.)

 

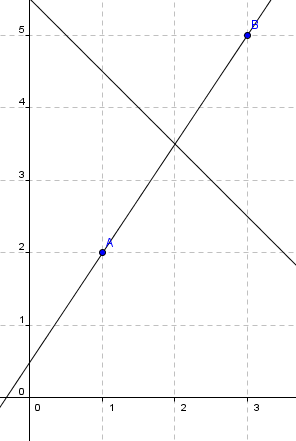
Das Bild bestätigt den Schnittpunkt (2, 3.5).