Durch die Punkte P1 und P2 verläuft eine Gerade, gib die Gleichung der linearen Funktion an

Question

Durch die Punkte P1 (0;-4) und P2(5;-6) verlaufen eine Gerade, die Graphen einer linearen Funktion ist.

B) Geben sie die Gleichung der Funktion an

 

und dann noch:

Lösen Sie das folgende Gleichungssystem rechnerisch und grapfisch.

I 3=x+y

II y=1/4x -2

 

und die letzte:

Gegeben ist das Gleichungssystem I x+y=6

II y=2x-3

a) Lösen Sie das Gleichungssystem rechnerisch.

 

 

Das wären die 3 Aufgaben,meiner Prüfungsvorbereitung mit denen ich leider überhaupt nicht klar komme. Ich hoffe hier kann mir geholfen werden.

Answer 1

Durch die Punkte P1 (0;-4) und P2(5;-6) verlaufen eine Gerade, die Graphen einer linearen Funktion ist.

B) Geben sie die Gleichung der Funktion an

Da ich den Y-Achsenabschnitt habe (P1) brauche ich nur noch die Steigung zwischen den Punkten.

m = (y1 - y2) / (x1 - x2) = (-6 - (-4)) / (5 - 0) = -2/5 = -0,4

f(x) = mx + b = -0,4x - 4

 

Lösen Sie das folgende Gleichungssystem rechnerisch und grapfisch.

I 3 = x + y

II y = 1/4x - 2

Da eine Gleichung (II) schon nach einer Unbekannten aufgelöst ist, kann man prima das Einsetzverfahren nutzen. D.h. ich setze 1/4x - 2 für das y in der ersten Gleichung ein.

3 = x + (1/4x - 2)

3 = 5/4 x - 2

5/4 x = 5

x = 4

y = 1/4x - 2 = -1

 

Um das zu zeichnen löst man sich die erste Gleichung auch noch nach y auf

I 3 = x + y

y = 3 - x

y = 1/4x - 2

 

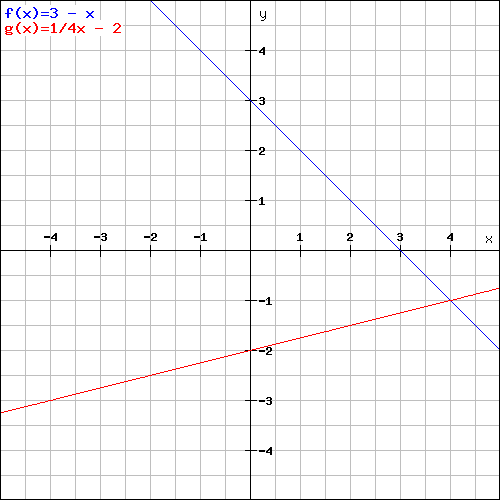
und die letzte:

Gegeben ist das Gleichungssystem

I x + y = 6

II y = 2x - 3

a) Lösen Sie das Gleichungssystem rechnerisch.

Auch hier nutzen wir wieder das Einsetzverfahren

x + (2x - 3) = 6

3x - 3 = 6

3x = 9

x = 3

y = 2x - 3 = 3

 

Answer 2

1. die beiden Punkte in die Normalform der Geradengleichung  eingeben (y=mx+b, oder auch y= ax+b)

         -4=0*m+b       ⇒b=-4 in die zweite Gleichung einsetzen

        -6=m*5-4         | +4 ,/5

     -2/5=m            

      Die Gleichung lautet     y=-2/5 x-4

 

2. Gesucht ist der Schnittpunkt der beiden Gleichungen. dafür  beide nach y  umformen und gleichsetzen

        3=x+y  ⇒  y=3-x

        y=1/4 x-2

    3-x=1/4x-2        |+2, +x

       5= 5/4x         ⇒x=4     und y= -1        S(4|-1)

       Zeichnerisch

 

3. Schnittpunkt der beidenGleichungen finden.

      x+y=6     y=6-x in die zweite einsetzen

      6-x=2x-3  |+x; +3

         9=3x             ⇒x=3    y=3    S(3|3)

 

 

Comments

die gezeigte Mühe ist lobenswert; obwohl ich die Aufgabe nicht gestellt habe, lerne ich daraus!!!