Nullstelle berechnen! Hilfe bei f(x)= 0,5x3 -4,5x2 +12x -9

Question

Ermitteln Sie alle Nullstellen von f und geben Sie diese exakt an.

f(x)= 0,5x^3 -4,5x^2 +12x -9

Answer 1

Wir dürfen keine Polonymdivision benutzen (im Jahre 2013)

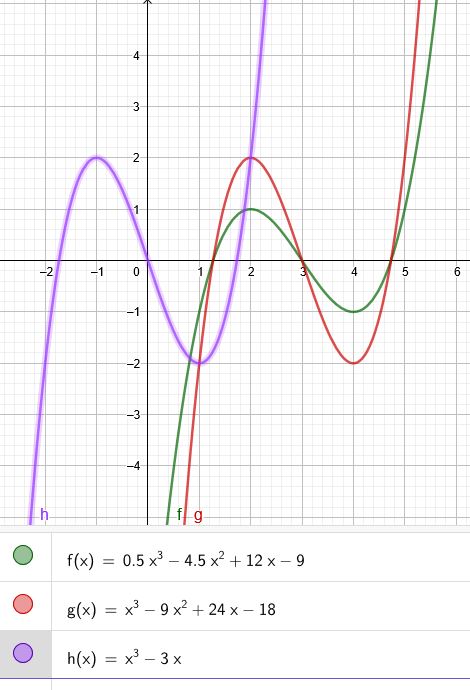
$f(x)= 0,5x^3 -4,5x^2 +12x -9$

$f´\frac{a}{b}(x)= 1,5x^2 -9x+12$

$1,5x^2 -9x+12=0$

$x_1=2$       $f(2)=1$

$x_2=4$      $f(4)=-1$

Kubische Parabeln sind punktsymmetrisch zum Wendepunkt.

$W( \frac{4+2}{2}| \frac{-1+1}{2})$   $W( 3| 0)$ Der Wendepunkt ist somit auch eine Nullstelle.

$0,5x^3 -4,5x^2 +12x -9=0$ → $x^3 -9x^2 +24x -18=0$

Die Nullstellen von $g(x)$ sind identisch mit den Nullstellen von $f(x)$

Ich verschiebe den Wendepunkt $W( 3| 0)$→$W´( 0| 0)$

Somit wird aus  $g(x)= x^3 -9x^2 +24x -18$  →

→$h(x)= (x+3)^3 -9*(x+3)^2 +24*(x+3) -18$

$h(x)=x^3+9x^2+27x+27 -9x^2-54x-81 +24x+72 -18$

$h(x)=x^3-3x$

$x^3-3x=x*(x-N)*(x+N)=x*(x^2-N^2)=x^3-N^2*x$

Koeffizientenvergleich ergibt  $N^2=3$→  $N_1=-\sqrt{3}$    $N_2=\sqrt{3}$

Ich verschiebe diese Nullstellen nun um 3 Einheiten nach rechts:

Nullstellen von $f(x)$  $N_1=-\sqrt{3}+3$  $N_2=3$   $N_3=\sqrt{3}+3$

Comments

Der Wendepunkt ist somit auch eine Nullstelle.

Da hast du aber Glück gehabt.

---

Da hast du aber Glück gehabt.

Fortuna fortibus favet , v.a. die Retter der quadratischen Ergänzung.

Answer 2

Vorschlag; die Dezimalzahlen "verschwinden "zu lassen, die Funktion mit 2 multipliziern

x³-9x²+24x-18 =0      durch Polynomdivision die erste Nullstelle finden , da in den  Parametern die Teiler 2 und 3 enthalten sind , mit  3 probieren

(x³-9x²+24x -18).(x-3)= x² -6x+6        erste Nullstelle   x₁=3

nun die pq-Formel anwenden

x_2,3= 3±√(9-6)                                                               x₂=3+√3  =4,732

                                                                                     x₃=3-√3    =1,2679                              

Comments

Wir dürfen keine Polonymdivision benutzen

---

Welche Verfahren  werden im Unterricht benutzt?