Einfaches Matrixexponential lösen!

Question

Hallöle,

Ich stecke gerade tief in der Prüfungsvorbereitung und komme bei den Matrixexponentialen nicht weiter.

Da unsere Analysis III Vorlesung irgendwie total verplant ist haben wir nice richtig gelernt wie man das macht.

Das soll gelöst werden:

 

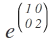
Da das eine Diagonalmatrix ist, müsste die Lösung doch sein:

 

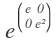
Das hatte Ich auch herausbekommen, als Ich die Reihenentwicklung gemacht hatte.

Nur ist das irgendwie nicht richtig.

WolframAlpha zeigt auch  was anderes:

https://www.wolframalpha.com/input/?i=exp%28{{1%2C0}%2C{0%2C2}}%29

Wo liegt der Fehler?

PS: Das ganze mit der Jordanschen Normalform hatten wir alles nicht, weswegen Ich den Weg über die Reihenentwicklung bevorzugen würde.

Gruß

Answer 1

Was hier vorher stand, war natürlich Blödsinn.
$$exp\begin{pmatrix} 1 & 0 \\ 0 & 2\end{pmatrix} = \begin{pmatrix} exp(1) &0 \\ 0 & exp(2)\end{pmatrix} = \begin{pmatrix} e & 0 \\ 0 & e^2\end{pmatrix}$$

Comments

Das deckt sich aber nicht mit Wikipedia:

https://de.wikipedia.org/wiki/Matrixexponential

".. indem man die übliche Exponentialfunktion auf jeden Eintrag der Hauptdiagonalen anwendet:"

---

Du hast natürlich recht, ich habe meine Antwort korrigiert. Das mit WolframAlpha ist ein wenig merkwürdig. Ich schau mir das mal an und schreibe, wenn ich die Lösung gefunden habe.

---

Bisher war WolframAlpha immer sehr intuitiv und "wusste" was man meint, aber scheinbar musst du "MatrixExp" nutzen: https://www.wolframalpha.com/input/?i=MatrixExp+%7B%7B1%2C0%7D%2C%7B0%2C2%7D%7D

Du meintest "Nur ist das irgendwie nicht richtig. WolframAlpha zeigt auch  was anderes". Was meinst du mit "nur ist das irgendwie nicht richtig"? Kamst du nur durch WolframAlpha darauf oder gibt es noch andere, die was anderes behaupten?

---

Achso okay,
Naja der Korrekteur der Übungsaufgaben hat das als Falsch markiert.

Wird wohl den selben Fehler in WoflramAlpha gemacht haben :D