"Ähnlich" bedeutet, dass alle Seiten mit dem gleichen Faktor skaliert sind.
Hat das Dreieck davor also die Seiten a, b und c, dann hat es jetzt die Seiten
a+a/3 = 4a/3
b+b/3 = 4b/3
c+c/3 = 4c/3
Ein Beispiel dafür ist das folgende Bild:
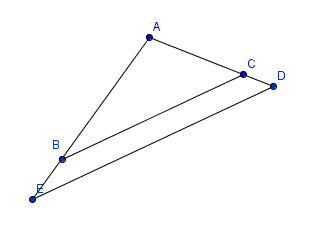
Die beiden Dreiecke ABC und AED sind ähnlich, AED ist um den Faktor 4/3 größer als ABC.
Der Flächeninhalt des Dreiecks ist nun 1/2*gh, wobei g die Länge einer Grundseite und h die Länge der darauf stehenden Höhe ist.
Ich zeichne das einmal ein:
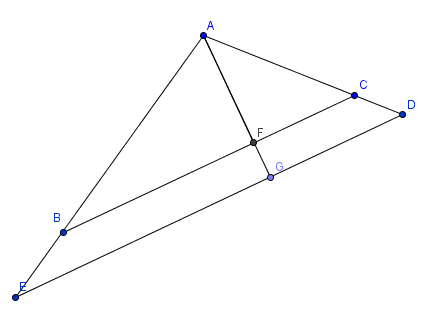
Für den Flächeninhalt f des kleinen Dreiecks gilt also:
f = 1/2 * |CB| * |FA|
Für den Flächeninhalt F des großen Dreiecks:
F = 1/2 * |ED| * |GA|
Wir wissen bereits, dass |ED| = 4/3*|CB| ist, denn die Seiten des Dreiecks wurden alle um ein Drittel vergrößert.
Wie sieht aber das Verhältnis von |FA| und |GA| aus?
Nach dem Strahlensatz gilt
|AD|/|AC| = |GA|/|FA|
Das Verhältnis links ist aber bekannt, denn |AD| = 4/3* |AC| also |AD|/|AC| = 4/3
Also gilt auch:
4/3 = |GA|/|FA| |*|FA|
|GA| = 4/3 |FA|
Setzt man alles das, in die Formel für F ein, so folgt:
F = 1/2 * |ED| * |GA|
F = 1/2 * 4/3*|CB| * 4/3 * |FA|
F = 16/9 * (1/2 * |CB|*|FA|)
F = 16/9 * f
Setzt man nun f=240 ein, so erhält man:
F = 16/9 * 240 = 1280/3 ≈ 426.67
Das große Dreieck ist also rund 426.67 cm2 groß.