Extrema trigonometrischer Funktion mit Betrag: f(x):= | sin (x)*cos(x) |?

Question

Ich brauche Hilfe bei der folgenden Aufgabe:

Es sind die Extrema der Betragsfunktion /sin (x)*cos(x)/ zu finden. Ich weiß nicht recht wie ich mit den betragsstrichen in diesem Fall umgehen soll. Ich habe sie zunächst weggelassen und bin zu dem Ergebnissen gekommen, dass die Nullstellen bei x= 1/4pi+npi/ 2 liegen müssten. Ich glaube aber das ist nicht ganz richtig..

Comments

"Nullstellen bei x= 1/4pi+npi/ 2 liegen müssten "

Das sind keine Nullstellen. Du hast hier offenbar Extremalstellen gefunden. Überlege dir, weshalb das so ist. Bestimme die y-Koordinaten deiner Hochpunkte und mach dich auf die Suche nach den Tiefpunkten. 

Answer 1

 

bekannte Formel:  sin(2x) = 2 • sin(x) • cos(x) → sin(x) • cos(x) = 1/2 • sin(2x).

Solche Formeln findest du z.B. hier (2.10 im Inhaltsverzeichnis):

https://de.wikipedia.org/wiki/Formelsammlung_Trigonometrie

→   | sin(x) • cos(x) |  =  | 1/2 • sin(2x) |

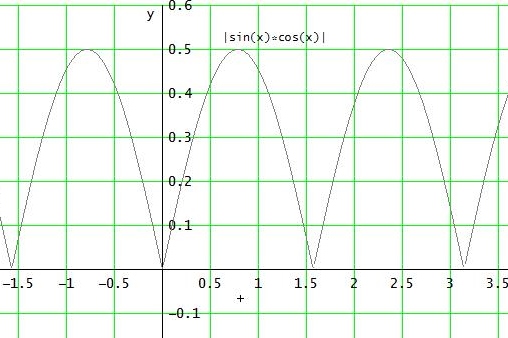
[ Verlauf des Arguments wie Sinusfunktion mit der Periode 2π/2 = π und der Amplitude 1/2. Wegen der halben Periodenlänge halbieren sich die x-Werte der Nullstellen und Extrempunkte. Die negativen . Anteile unter der x-Achse werden durch den Betrag positiv ("nach oben geklappt") ]

Deshalb liegen die Maxima in den Punkten ( π/4 + k • π/2 | 1/2 )   und

die Minima in den Nullstellen ( k • π/2 | 0 )   mit k∈ℤ

Gruß Wolfgang

Comments

Ich danke dir für die Antwort, aber noch verstehe ich nicht ganz was du da gemacht hast. Eine etwas ausführlichere Antwort wäre super! Ich danke dir vielmals !!

---

Was genau verstehst du nicht? Der erste Schritt beruht auf der Doppelwinkelformel. Findest du vermutlich in deinen Unterlagen oder unter den Additionstheoremen der trigonometrischen Funktionen (-> Wikipedia).

---

Habe die Antwort ergänzt. Zum Verständnis des Graphen von 1/2 • sin(2x)  kannst du dir eine Wertetabelle machen und ihn zeichnen.