Tangente an einer Ellipse (implizites Differenzieren)

Question

Ich fange gerade an Taylorpolynome zu lernen, dabei gab es einen kleinen Einschub zum Thema Implizites Differenzieren mit genau einer Aufgabe.

Bestimmen Sie die Tangente an der Ellipse:

X²/4 + y²/3 =1

im Punkt P(1,y) , y>0 durch implizites Differenzieren.

Mein Ansatz:

∂/∂x (X²/4) + ∂/∂x(y²/3) = ∂/∂x(1)

x/2 + 2/3 yy' = 0

y'=-3x/4y

Frage 1: Hab Ich richtig differenziert?
Frage 2: Müsste ich durch das Differenzieren nicht auch schon gleichzeitig Steigung m der Tangente haben? bzw. wie komme ich auf Die Lösung von t : y = -1/2 x +2

Answer 1

Die Tangente geht durch den Punkt P(1;3/2) und hat die angegebene Gleichung y = -1/2x+2. Das habe ich ganz ohne implizites Differenzieren herausgefunden. Die Ellipse entsteht aus dem Kreis mit der Gleichung y²+x² =4, indem man mit dem Faktor √3/2 in y-Richtung staucht. Die Urbild-Tangente an den Kreis vor der Stauchung geht durch den Punkt (1/√3) und hat die Gleichung y=-x/√3+4/√3 und den Punkt Q(4/0). Das ist ein Fixpunkt bei Stauchung.. Die Punkte P und Q führen zu der angegebenen Tangentengleichung

Comments

Danke, aber wie komme ich auf die Tangetengleichung durch implizites Differenzieren?

---

Rechne zunächst y aus, indem du x=1 einsetzt, und bestimme dann die Steigung der Tangente.

Answer 2

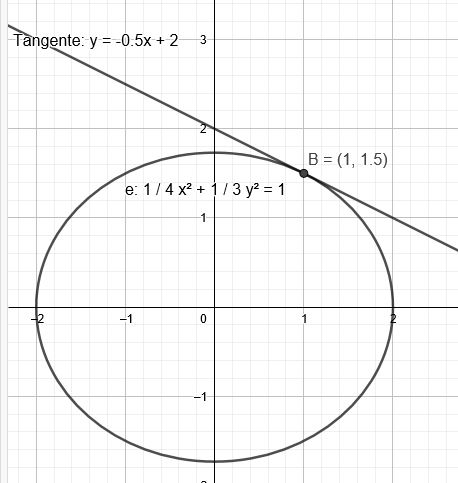
$f(x,y)=\frac{1}{4} x^2 + \frac{1}{3}y^2 -1$

implizites Differenzieren:

$f'(x)=-\frac{f_x(x,y)}{f_y(x,y)}$

$f_x(x,y)=\frac{1}{2} x$

$f_y(x,y)=\frac{2}{3} y$

$f'(x)=-\frac{\frac{1}{2} x}{\frac{2}{3} y}$   mit Berührpunkt $B(1|1,5)$:

$f'(1)=-\frac{\frac{1}{2} }{\frac{2}{3} \cdot 1,5}=-0,5$

Tangente mit der Punkt-Steigungsform der Geraden:

$\frac{y-1,5}{x-1}=-0,5$

$y=-0,5x+2$