Kosten-, Gewinn- und Erlösfunktionen. Degressiv steigende Gesamtkosten eines Betriebes

Question

Bräuche Hilfe bei Aufgabe 2

Komme leider nicht weiter .

Comments

EDIT: Habe nun das neue Bild oben eingefügt und die Fragestellung auf Aufgabe 2 beschränkt. Vgl. "Schreibregeln" im grünen Balken unten.

Falls du 3 tatsächlich auch noch brauchst, wenn du Aufgabe 2 begriffen hast, gib in der Frage dann bitte an, bis wohin du selbst kommst und was du genau für einen Tipp brauchst. 

---

Ok danke..Bräuchte trotzdem Hilfe bei der Aufgabe 

Answer 1

K(x) = ax² + bx + 40   [GE]     (Fixkosten)

K(10) = 200  ⇔  100·a + 10·b + 40 = 200

K(5) = 165     ⇔  25·a + 5·b + 40 = 165

Das LGS  hat  die Lösung   a = - 9/5  und   b = 34

Gesamtkosten:    K(x) = - 1,8·x² + 34x + 40                    

Variable Kosten:  K_V(x) = - 1,8·x² + 34x

Variable Stückkosten:  k_v (x) =  - 1,8·x 

      jeweils   D_math = ℝ  ;  D_ök =  [ 0 ; 10 ]   (wegen der Kapazitätsgrenze 10 GE)

      jeweils   D_ök =  [ 0 ; 10 ]   (wegen der Kapazitätsgrenze 10 GE)

Stückkosten:         k(x) = K(x) / x = - 1,8·x + 34 + 40/x

                         D_math = ℝ \ {0}   ;  D_ök =  ] 0 ; 10 ]  

D_ök =  [ 0 ; 10 ]   (wegen der Kapazitätsgrenze 10 GE)

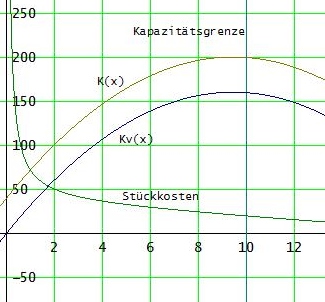
Für die Wertebereiche gilt:

K(x):  Untergrenze = 40  ;  Obergrenze K(85/9) ≈ 200.555 [GE]

      wegen K'(x) = 34 - 18·x/5 = 0 →  x = 85/9  ist  (85/9 | 200.555) das Kostenmaximum

K_V(x): Untergrenze = 0  ;  Obergrenze K(85/9) - 40  = 160,555 [GE]

Stückkosten:  ] a ; k(10) ] , a kann nicht festgelegt werden, weil man nicht weiß, wie weit sich x der Zahl 0 nähern kann.  x=0 ist eine Polstelle

Gruß Wolfgang