Hallo fleißiges Mädchen,
wie versprochen:
die Gedankengänge von Mathecoach kann ich im Moment leider nicht nachvollziehen. Die gleichen Ergebnisse erhalte ich wie folgt:
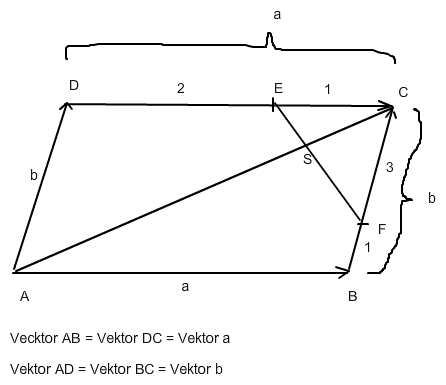
ES ... sind die Verbindungsvektoren der Punkte, a und b sind Vektoren
Suche ein Dreick mit dem Teilpunkt S als Eckpunkt ( z.B. ΔESC)
ES + SC + CE = 0 (geschlossene Vektorkette)
ES = x * EF = x * (1/3·a - 3/4·b) (x = Bruchteil der Länge von EF)
SC = y * AC = y * (a + b) ((y = Bruchteil der Länge von AC)
CE = - 1/3·a
in erste Gleichung einsetzen:
x * (1/3·a - 3/4·b) + y * (a + b) - 1/3·a = 0
Ausmultiplizieren und dann a und b ausklammern:
( 1/3·x + y -1/3 ) * a + ( -3/4·x + y ) * b = 0
wegen der linearen Unabhängigkeit von a und b haben die Klammern dern Wert 0
1/3·x + y -1/3 = 0 und -3/4·x + y = 0
die Lösungen des Gleichungssystems sind
.......
x = 4/13 und y = 3/13
Setzt man x und y oben bei ES und SC ein, hat man
Also: ES = 4/13 · EF und SF = 9/13 · EF
SC = 3/13 · AC und AS = 10/13 · EF
Strecke ES / Strecke SF = 4 / 9
Strecke AS / Strecke SC = 10 / 3
Wenn du noch Fragen hast, dann los!
VLG Wolfgang