Hier einmal eine Grafik, die es zusammenfasst:
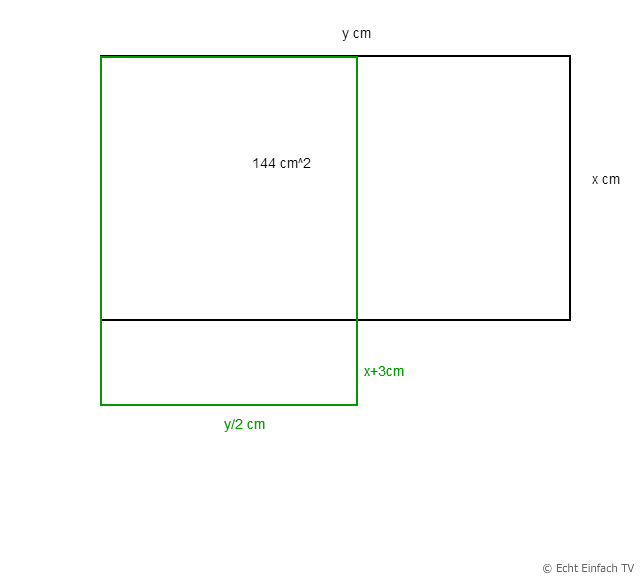
Du hast gesagt: Neues Feld (Grün) zu Altem mit Flächeninhalt 144 cm2 (Schwarz) verhält sich wie 5 zu 8.
Das bedeutet mal, dass das neue Feld grösser sein muss als das alte Rechteck, und dies im Verhältnis 5/8. Jetzt kann man mal den Flächeninhalt den Neuen ausrechnen!
144/x = 5/8
Via Kreuzprodukt folgt: x=144/5*8= 230.4 cm2.
Jetzt muss man noch die Seiten ausrechnen:
x*y=144; (x+3)*y/2=(xy+3y)/2=230.4
Dies habe ich bei WolframAlpha eingegeben, das Ergebnis für x ist 540 / 397; für y 1588 / 15, was für x ungefähr 1.3602cm und für y etwa 105.866666666...cm entspricht.
ACHTUNG: Ich habe nicht genau gelesen und cm als Einheit genommen!