teile das Intervall in 4 Bereiche und berechne im Mittelpunkt eines jeden Bereichs den Funktionswert. Dieser Funktionswert gibt die Höhe des jeweiligen Rechtecks an und die Breite \(h\) ist die Breite des ganzen Intervalls (=2) durch die Anzahl der Bereiche - hier =4 - also \(h=2/4=0,5\)
Folgendes Bild zeigt das:
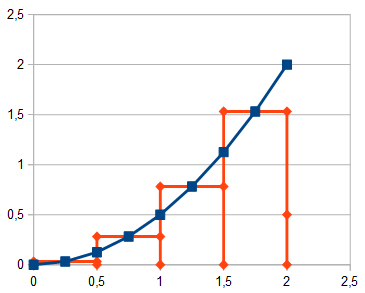
Jetzt noch die Flächen der Rechtecke addieren
| x | f(x) | A=f(x)*0,5 |
| 0,25 | 0,03125 | 0,015625 |
| 0,75 | 0,28125 | 0,140625 |
| 1,25 | 0,78125 | 0,390625 |
| 1,75 | 1,53125 | 0,765625 |
| Summe= | 1,3125 |
Der exakte Wert ist \( \int_0^2 \frac{1}{2} x^2 dx = \frac{4}{3}\approx 1,333\)
Die Rechnung mit 8 Rechtecken ergibt einen Wert von \(\approx 1,328\).
Gruß Werner