Hallo Claudia,
a)
rechnerische Bestimmung des Schnittpunkts:
du musst f(x) und g(x) gleichsetzen:
1/3 x + 2,5 = -2x - 1
Auf beiden Seiten der Gleichung addierst du jetzt 2x und subtrahierst 2,5
1/3 x + 2,5 + 2x - 2,5 = - 2x -1 + 2x - 2,5
diese Glieder heben sich auf:
1/3 x + 2x = -1 - 2,5
7/3 x = -3,5
Jetzt dividierst du beide SdG durch 7/3 ( = Multiplizieren mit 3/7):
x = -3,5 * 3/7 = -1,5
Einsetzen in eine der Geraden ergibt den y-Wert des Schnittpunkts:
z.B. y = g(-1,5) = - 2 * (-3,5) - 1 = 2
Schnittpunkt: S( -1,5 | 2 )
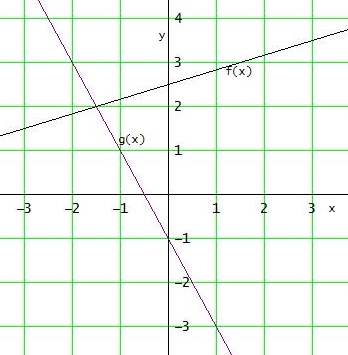
graphische Bestimmung von S
Du musst die beiden Geraden ins Koordinatensystem einzeichen. Dann kannst du den Schnittpunkt ablesen.
Dazu brauchst du von jeder Geraden zwei Punkte (x|y). Diese erhältst du , wenn du jeweils einen x-Wert in eine der Geradengleichungen einsetzt und den passenden Wert y = f(x) ausrechnest.
z.B. für Gerade f: x = 0 → y = 1/3 * 0 + 2,5 = 2,5 → P1 ( 0 | 2,5 )
x = 3 → y = 1/3 * 3 + 2,5 = 3,5 → P2 (3 | 3,5 )
für Gerade g genauso .... → P1 = (0 | -1) und P2 = ( 1 | -3 )
Gruß Wolfgang