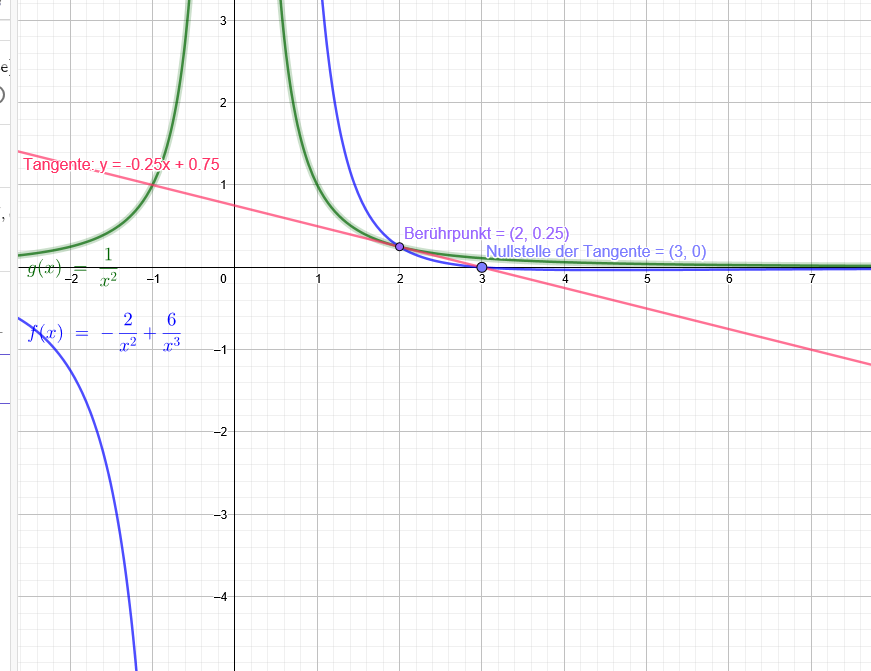
"Die Tangente an den Graphen von g(x)=\( \frac{1}{x^2} \) im Punkt P (x₀|y₀) hat eine Nullstelle bei x=3"
g´(x)=-\( \frac{2}{x^3} \)
\( \frac{y-0}{x-3} \) =-\( \frac{2}{x^3} \)
f(x)=-\( \frac{2}{x^2} \)+\( \frac{6}{x^3} \)
f(x)=g(x)
-\( \frac{2}{x^2} \)+\( \frac{6}{x^3} \)=\( \frac{1}{x^2} \)
-\( \frac{3}{x^2} \)+\( \frac{6}{x^3} \)=0 | • \( x^{3} \)
-3x=-6
x=2 →y=\( \frac{1}{4} \)
Berührpunkt P(2|\( \frac{1}{4} \))