Hallo beater_girl,
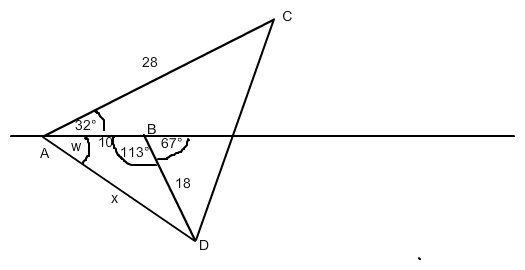
Kosinussatz in ΔABD :
x = √( 102 + 182 - 2 * 10 * 18 * cos(113°) ) ≈ 23,763 [km]
Sinussatz in ΔABD :
sin(w) = 18 / 23,763 * sin(113°) ≈ 0,6973 → w ≈ 44,2°
Kosinussatz in ΔADC:
CD = √( 23,7632 + 282 - 2 * 23,763 * 28 * cos(76,2°) ) [ 76,2° = 32° + 44,2° ]
CD ≈ 32,113 [km]
Gruß Wolfgang