Rekonstruktion Ganzrationaler Funktion Garagenauffahrt 5)

Question

ich habe das Proble dass ich aus meiner Aufgabe(siehe Bild Aufgabe 5) nur 3 Gleichungen ablesen kann. Bisher habe ich f''(3)=0, f(0)=0 und f(6)=1. Allerdings braucht man ja für eine Funktion 3. Grades 4. Wie finde ich die letzte heraus?

.

Answer 1

Sorry, ich hatte f '(0) = 0 gelesen, was wegen "knickfrei " auch richtig ist.

Comments

Okay. Und warum muss ich dort die erste Ableitungen nutzen? 

---

Das ist nicht "müssen" .

Aber du kannst nutzen, dass der Graph bei x=0 ein lokales Minimum hat.

Du kannst auch die Symmetrie ausnützen und f(3) nehmen, vgl. andere Antwort.

Answer 2

Wie wäre es mit f(3)=1/2 ?

Answer 3

Ich habe sogar 5: Die drei von dir: f''(3)=0, f(0)=0 und f(6)=1. Außerdem f '(0)=0 und f '(6)=0.

Answer 4

f(0) = 0

f'(0) = 0

f(6) = 1

f'(6) = 0

Ich hätte es aber wie folgt gemacht

f(x) = a·x^2·(x - b) = a·x^3 - a·b·x^2

f'(6) = 0 --> 12·a·(9 - b) = 0 --> b = 9

f(6) = 1 --> 36·a·(6 - b) = 1 --> 36·a·(6 - 9) = 1 --> a = -1/108

f(x) = -1/108·x^2·(x - 9) = 1/12·x^2 - 1/108·x^3

Comments

Auch folgendes ist möglich: Zunächst den Wendepunkt in den Ursprung setzen.

f(x) = ax^3 + bx

f(3) = 0.5

f'(3) = 0

a und b ausrechnen und dann die Funktion zurück verschieben.

f(x) = a(x - 3)^3 + b(x - 3) + 0.5

Answer 5

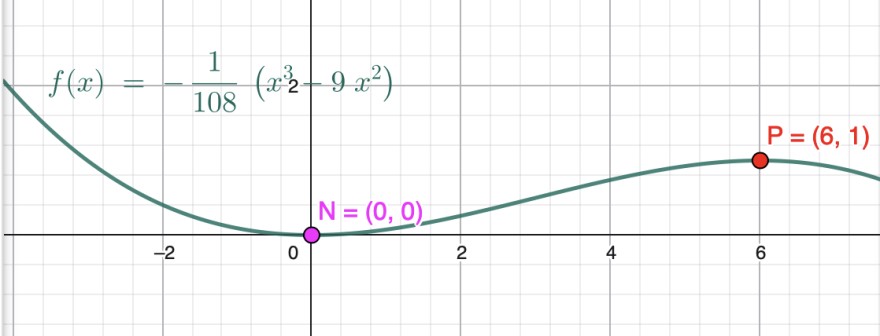
5).  Knickfrei bedeutet, dass der Graph  in N(0|0)  eine doppelte Nullstelle hat.  Dort ist die Tangente wegen des Extremum waagerecht. Ebenso auch in P(6|1) .

Linearfaktorenform:

\( f(x)=ax^2(x-N)=a(x^3-Nx^2) \)

waagerechte Tangente in P(6|...) Die Steigung ist dort m=0:    1. Ableitung Null setzen:

\( f'(x)=a(3x^2-2Nx) \)

\( f'(6)=a(108-12N)=0 \)

\(N=9 \)

\( f(x)=a(x^3-9x^2) \)

P(6|1) liegt auf dem Graphen:

\( f(6)=a(216-324)=-108a=1 \)

\(a=-\frac{1}{108} \)

\( f(x)=-\frac{1}{108}(x^3-9x^2) \)