Vom Duplikat:
Titel: Existiert ein Vektor x element aus R^3 mit ...,
Stichworte: lineare,algebra,vektoren
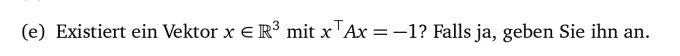
Ich habe wirklich gar keine Idee, wie man das lösen kann. Offensichtlich gilt es eine Gleichung zu lösen und zu guckeb ob ein Ergebnis rauskommt, was die Behauptung bestätigt. Ich weiß jetzt aber nicht genau wie diese Gleichung auszusehen hat.
x(transponiert) * A*x=-1
x soll der gesuchte Vektor sein nehme ich an(?)