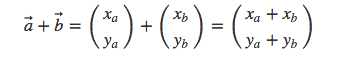Hallo Wolfgang, du hast ja ein super Gedächtnis :)
Ich grübel noch immer an der Aufgabe.Vielleicht kannst Du mir nochmal einen Tipp geben.
Also es geht darum, die höchst mögliche algebraische Struktur zu beweisen.
M = R X R = R 2
Und nun die Sturktur für (M,⊕)
⊕ := {(a,b)∈ M X M Ι a ⊕ b = (a1+b1,a2+b2)}
also ich wollte erstmal grundsätzlich verstehen, wie mann denn nun als Bsp. zwei Elemente dieser Menge addieren kann,
muss ich denn hier quasi als Bsp. ((1,2) , (3,4) ), ( (5,2), (3,8) )
(1,2) als a1 (3,4) als b1 (5,2) als a2 (3,8) als b2 ansehen und dann einfach nach diesem Prinzip ?